[OpenGL ES] 5강 : 렌더링 파이프라인, 카메라 공간, 뷰 변환(View Transform), 오른손 좌표계와 왼손 좌표계, 절두체

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

1. 렌더링 파이프라인은 크게 다음과 같은 순서로 진행된다 : Vertex Shader -> Rasterizer -> Fragment Shader -> Output Merger

2. Vertex Shader 는 각 정점에 대한 정보를 채워 Rasterizer 로 전달한다. Vertex Shader 의 역할은 오브젝트 공간에서 월드 공간(World Transform)으로, 월드 공간에서 카메라 공간(View Transform)으로, 마지막으로 카메라 공간에서 클립 공간(Projection Transform)으로 좌표계를 변환하는 것이다! 공간에 따라 왼손/오른손 좌표계를 사용하는데, 이를 제대로 변환하려면 z 축의 부호를 바꾸어주면 된다.

3. 카메라가 렌더링할 물체를 담는 공간을 절두체(View Frustum) 이라고 한다.

GPU 렌더링 파이프라인 개요

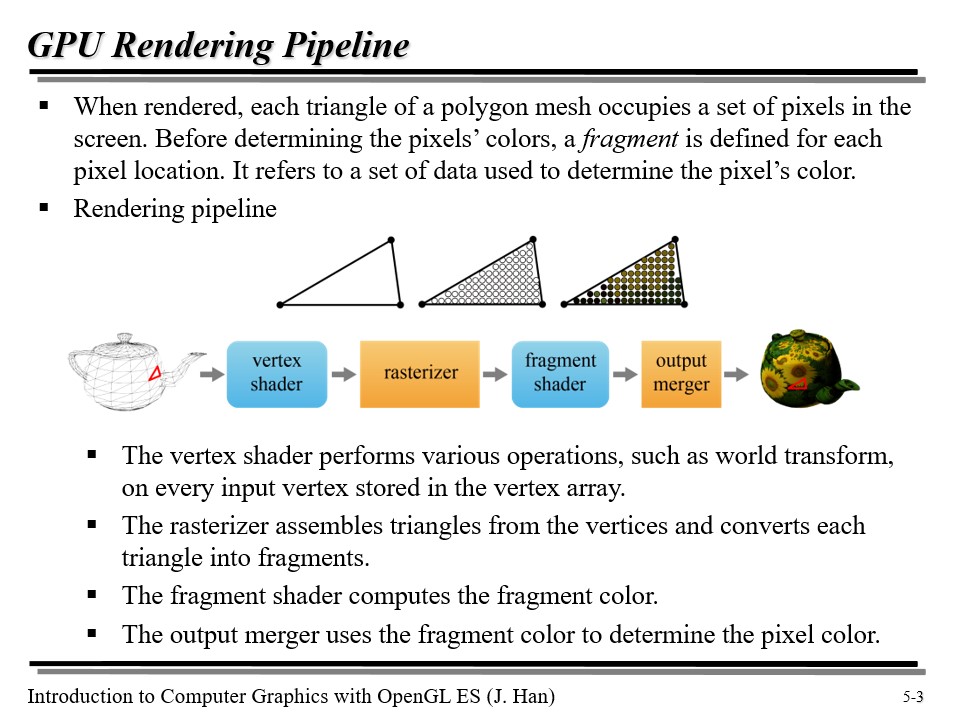
GPU 에서, 렌더링은 파이프라인 구조로 처리된다.
shader 는 사실 프로그램과 동의어이다. 우리는 파이프라인에게 두 프로그램을 제공해 주어야 하는데, 그것이 바로 vertex shader 와 fragment shader 이다. 반면, rasterizer 와 output merger 는 고정된 기능을 수행하는 녀석들이다(hard-wired 된 단계임).
파이프라인의 각 단계에 대한 자세한 설명은 포스팅을 하면서 점차 다룰 예정이므로, 여기서는 간단히 개요만 살펴보고 가도록 하자.

• vertex shader : vertex shader 는 vertex array 에 저장된 모든 input vertex 에 대해 '다양한' 연산을 수행한다.
• rasterizer : rasterizer 는 꼭짓점들로부터 삼각형을 만들고 각 삼각형을 fragment 로 만든다. fragment 는 삼각형의 픽셀 위치와 색상을 결정하는 데이터를 담게 된다.
• fragment shader : fragment shader 는 fragment color 를 계산한다(일반적으로 텍스쳐링과 라이팅을 수행함).
• output merger : output merger 는 fragment color 를 이용해 픽셀 컬러를 결정한다.

 

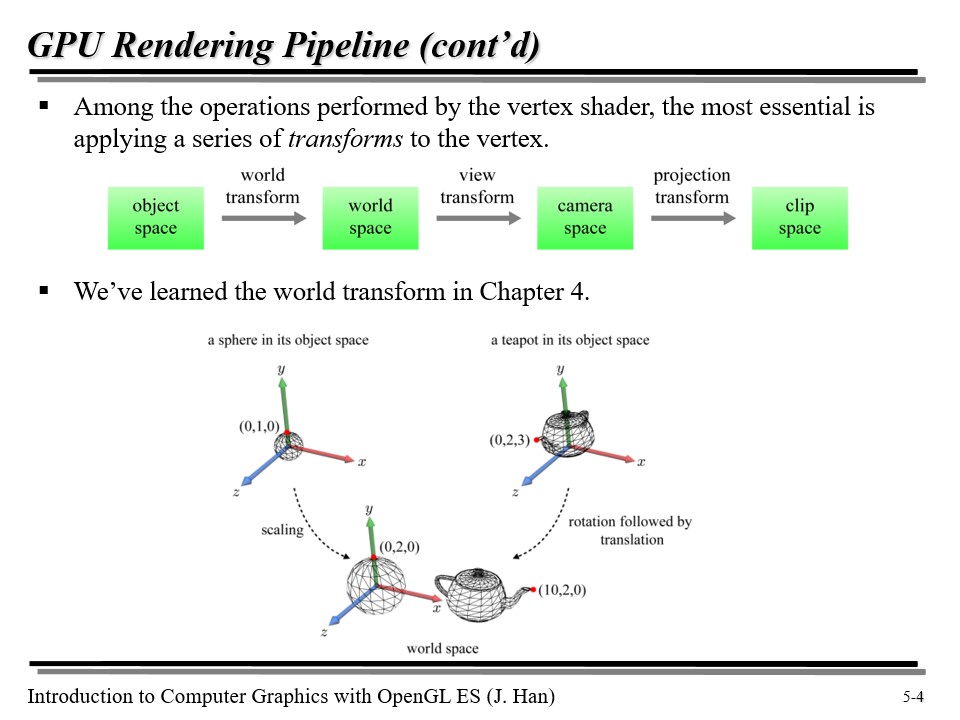
vertex shader 에 의한 연산 중 가장 중요한 것은 vertex 에 여러 변환(transform)을 수행하는 것이다.
총 3가지의 변환을 기억해 두자.

1. 월드 변환(World transform) : 오브젝트 공간에서 월드 공간으로의 변환
2. 뷰 변환(View transform) : 월드 공간에서 카메라 공간으로의 변환
3. 투영 변환(Projection transform) : 카메라 공간에서 클립 공간으로의 변환

그 중 월드 변환은 4강에서 이미 다룬 바 있다.
 
 

노멀 벡터의 월드 변환

4강에서 월드 변환에 대해 배우긴 했지만, 한 점(vertex)에 대한 변환밖에 다루지 않았었다. Vertex array 에 들어오는 중요한 정보 중 Vertex Normal 이 있는데, Vertex Normal 은 어떻게 변환하면 될까?
우리는 아핀 변환을 Scaling, Rotation, Translation 세 가지가 결합된 녀석임을 알고 있다. 또한 아핀 변환을 [L|t] 로 표현할 수 있다는 것도 알고 있다. 그런데 normal 은 벡터이므로, translation 에 영향을 받지 않는다. 즉, 우리는 L 만 고려하면 된다.
그런데 L 에 non-uniform 한 변환이 껴 있다고 해 보자. 위 예시에서 빨간색 선분은 xyz 공간에 있는 삼각형이 xy 평면과 부딪힌 단면이라고 가정하고 있다. 아래 그림처럼 말이다.

그런데 위 선분의 normal 벡터(연두색)인 (1/sqrt(2), 1/sqrt(2)) 에 non-uniform 한 scaling 을 적용하면, 해당 벡터는 더 이상 빨간색 선분과 수직을 이루지 않게 된다!
 

그렇다면 실제로 변환이 이루어졌을때, normal 벡터가 기존의 빨간색 선분에 수직인 성질을 유지시키려면 어떻게 해야 할까?
normal 이 삼각형과 수직이게 만드려면, 우리는 L 의 역행렬에 Transpose 를 취한(역행렬 + 전치행렬) 녀석을 곱해 주어야 한다.

만약 L 이 non-uniform 한 scaling 을 갖고 있지 않다면, normal 은 L 에 의해서도 변환이 제대로 이루어 진다.
그런데 L 을 곱하든, L 의 역행렬+전치행렬 버전을 곱하든 둘은 크기는 다를 수 있지만 같은 방향을 가리키게 된다. 따라서, 우리는 L^(-T) 를 곱하는 것이 상책이라는 것을 알 수 있다. 😅
결론 : Vertex Normal 은 L^(-T) 에 의해 변환된다. 그 후에 Normalize 를 거치면 단위 벡터가 된다!
 
 

카메라 공간과 뷰 변환(View Transform)

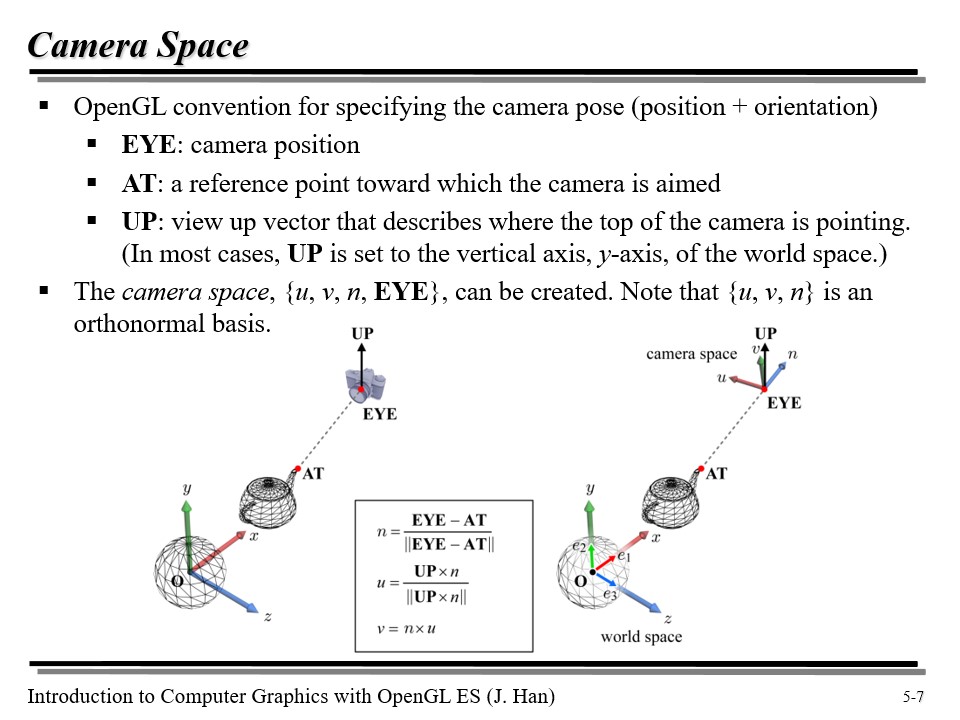
카메라 공간을 이해하기 위해서는 먼저 3가지 개념을 숙지해야 한다.

• EYE : 카메라의 위치
• AT : 카메라가 바라보고 있는 지점
• UP : 카메라의 끝이 가리키고 있는 벡터(왜냐면, 카메라가 살짝 기울어진 상태일 수도 있으니까!)

카메라 공간에서의 기저 벡터를 n, u, v 라고 하자. 각각은 다음과 같이 구할 수 있다 :

• n : EYE - AT 을 normalize 한 것. 벡터를 빼면 뺀 녀석이 출발점, 빼진(?) 녀석이 도착점이 된다. 즉, AT 에서 EYE 까지의 단위벡터!
• u : UP x n. 아까 UP 을 카메라가 위쪽으로 바라보고 있는 벡터라고 정의했었다. UP 과 n 은 수직일 것이다.
• v : n x u. 이전에 구한 두 벡터를 활용하면 간단히 구할 수 있다!

위의 세 기저벡터 u, v, n 과 EYE 가 카메라 공간을 정의하고 있다!
 

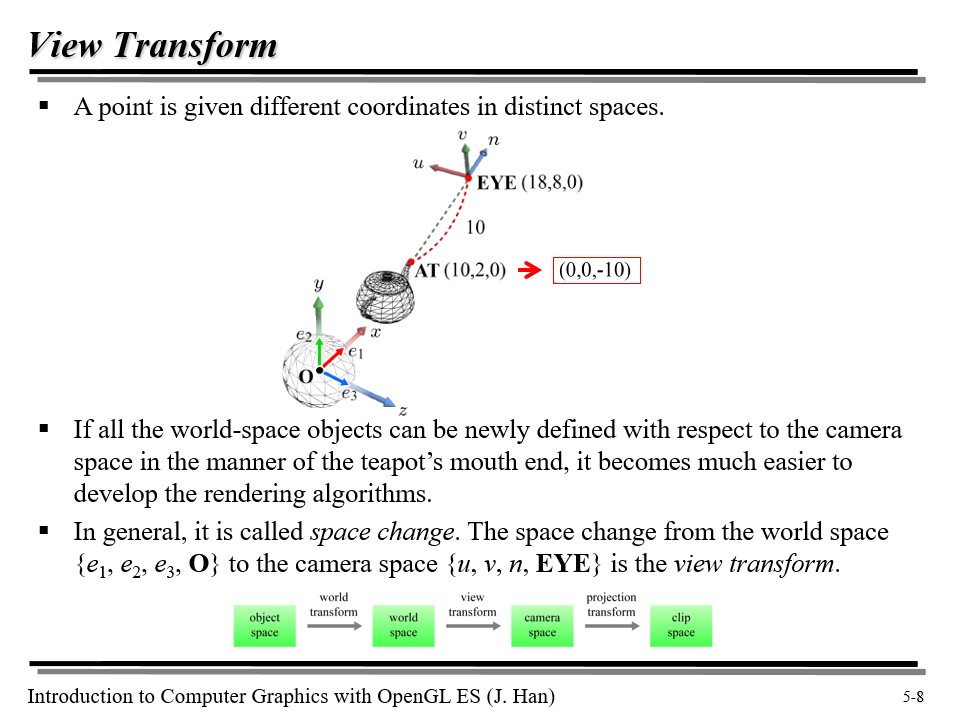
위 그림에서, 주전자 끝 점인 AT 은 (10, 2, 0) 으로 표현되고 있다. 그런데, 우리는 이 좌표를 카메라 공간에서의 좌표값으로 변환하고 싶다.
이때, AT 의 경우, u 와 v 축 값은 0일 것이다(잘 모르겠으면 그림을 다시 보자). 그리고 n 축의 값의 경우, 아까 우리가 n 을 AT 에서 EYE 로의 벡터(EYE - AT)으로 정의했으므로, AT 의 n 축 좌표값은 -10이 될 것이다! 왜 -10이냐면, (18, 8, 0) 과 (10, 2, 0) 사이의 거리가 10이고, 방향은 n 축에서 음의 방향이기 때문이다.
월드 공간에 있는 오브젝트들이 아까 주전자 끝의 점이 변환된 것처럼 카메라 공간으로 오게 만들면, 렌더링이 더욱 쉬워진다. 이처럼, 월드 공간에서 카메라 공간으로의 변환을 view transform 이라고 부른다!
 

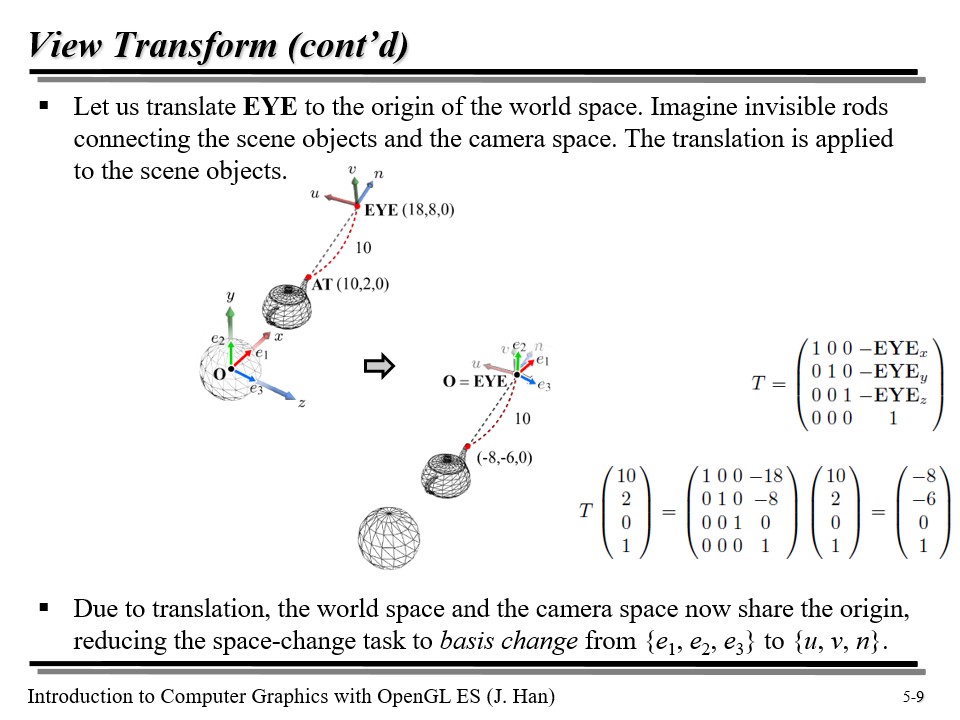
그렇다면 어떻게 모든 점을 한번에 잘 변환할 수 있을까? 일단, 씬에 있는 오브젝트들이 카메라 공간과 투명한 막대기로 붙어 있다고 상상하면서 진행해 보자.😄
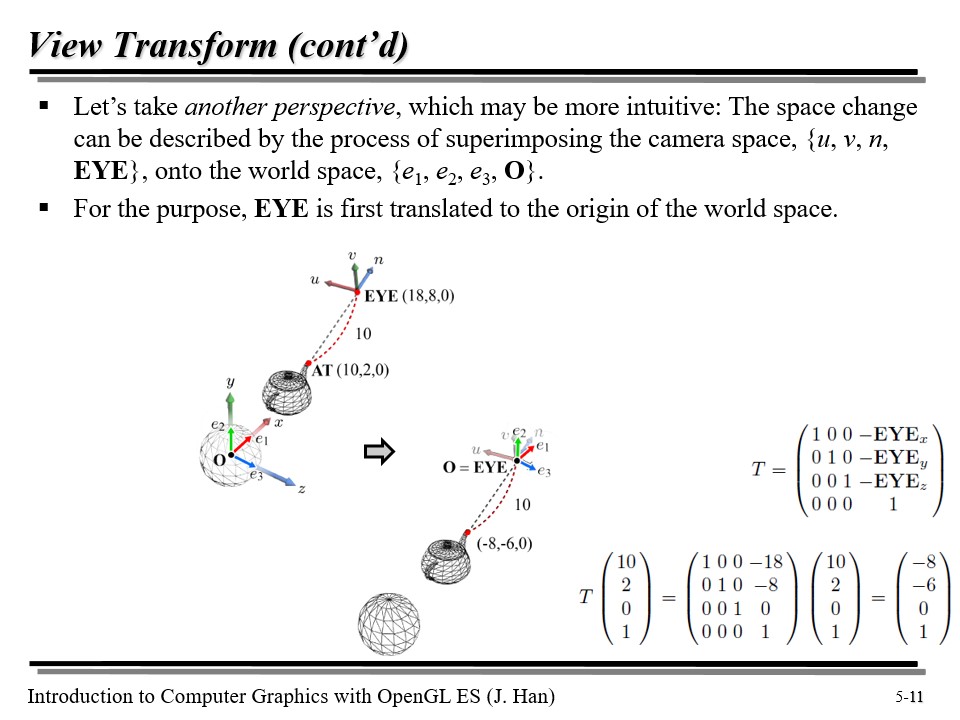
일단, EYE 를 월드 공간에서의 원점과 일치시켜 준다. 이를 위해서는 먼저 translation 을 해야 할 것이다!

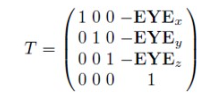
 그럼 이제 회전만 시키면 된다...
 

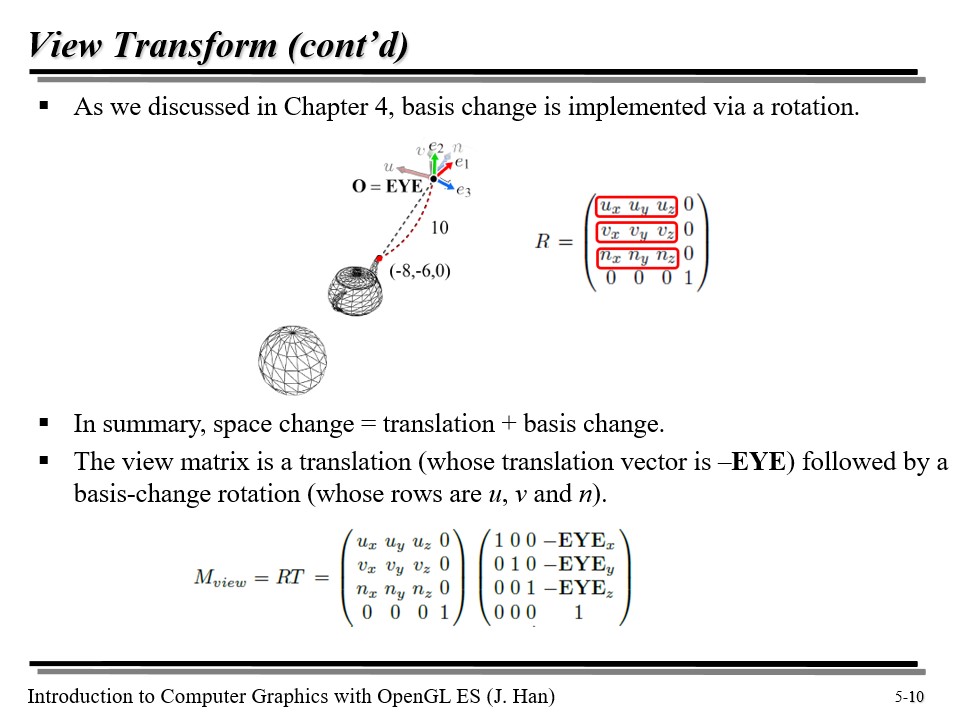
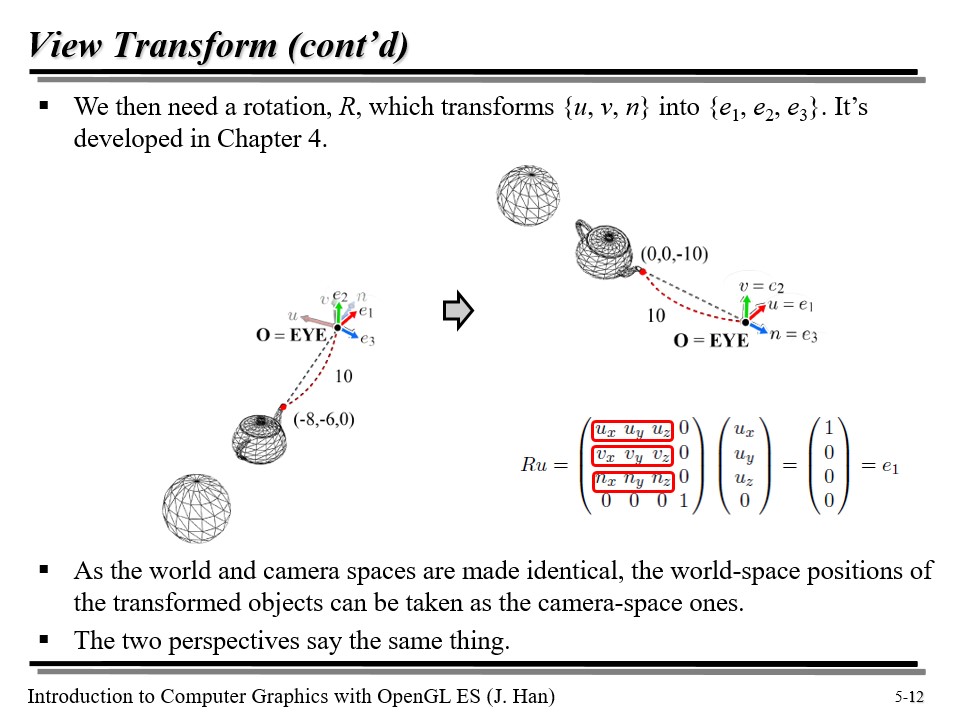
4강에서 다뤘듯이, 기저 변환은 회전을 통해 이루어진다. 이미 알듯이, 기저 벡터를 transpose 한 녀석을 곱하면 된다.
요약하면, 공간 변환은 translation 과 basis change 의 결합이다!

 

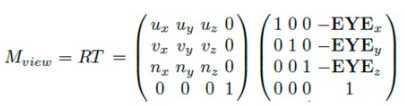
추가 페이지인데, 심심하면 더 읽어보자.
 

요것도 마찬가지.
 

위 그림은 RT 를 행렬식으로 더 자세히 표현한 것이다.
이러한 공간 변환은 매우매우 중요하다!
 

위의 행렬은 R 과 t 로 분리해서 생각할 수 있다!
 

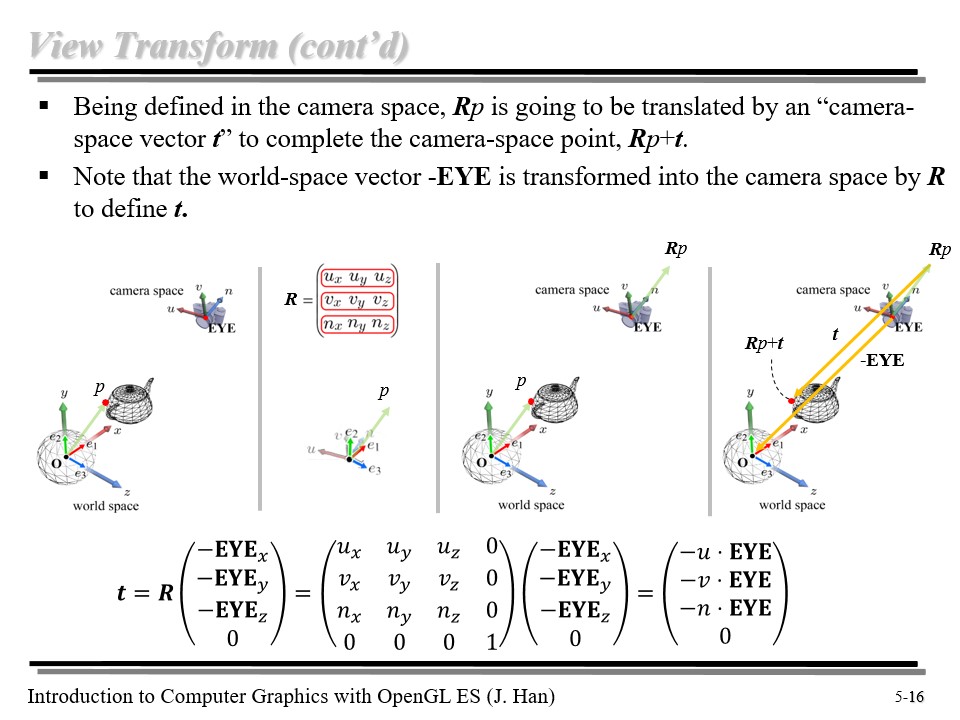
실제로는 R 에 p 값을 곱해서 벡터의 크기도 고려해 주어야 할 것이다.
 
 

오른손 좌표계와 왼손 좌표계

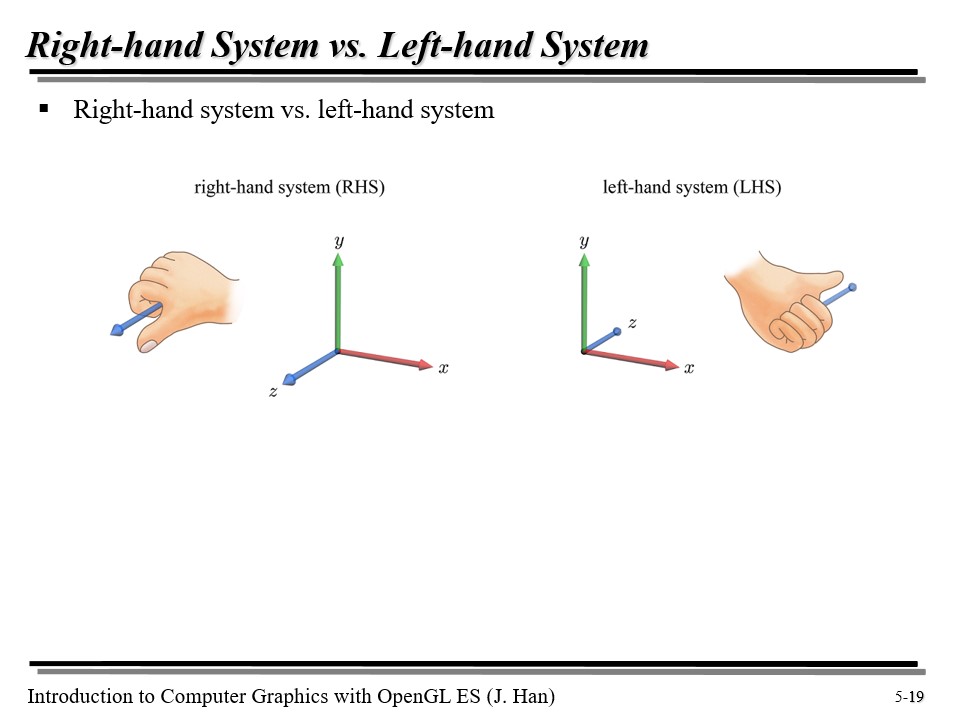
우리는 이전에 오른손 좌표계를 사용했다. 그런데 사실 왼손 좌표계를 쓰는 경우도 많다. 대표적으로 Direct X...
 

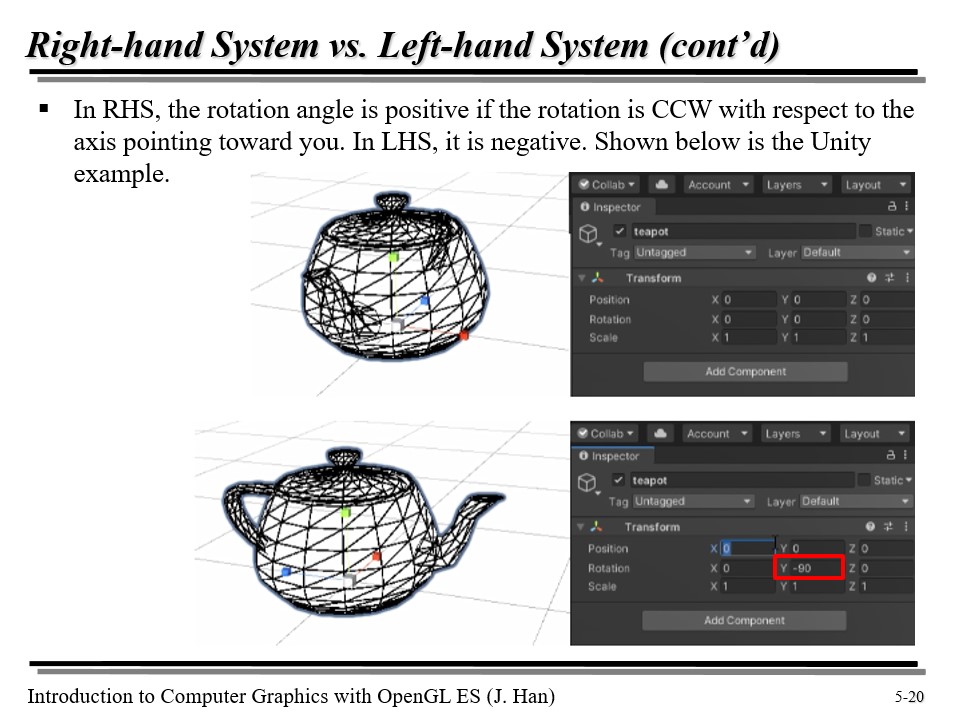
오른손 좌표계에서는 회전이 반시계로 이루어질 때, 회전각이 양수이다. 그리고 그 축은 나 자신을 가리킨다. 왼손 좌표계에서는 이게 반대이다.
 

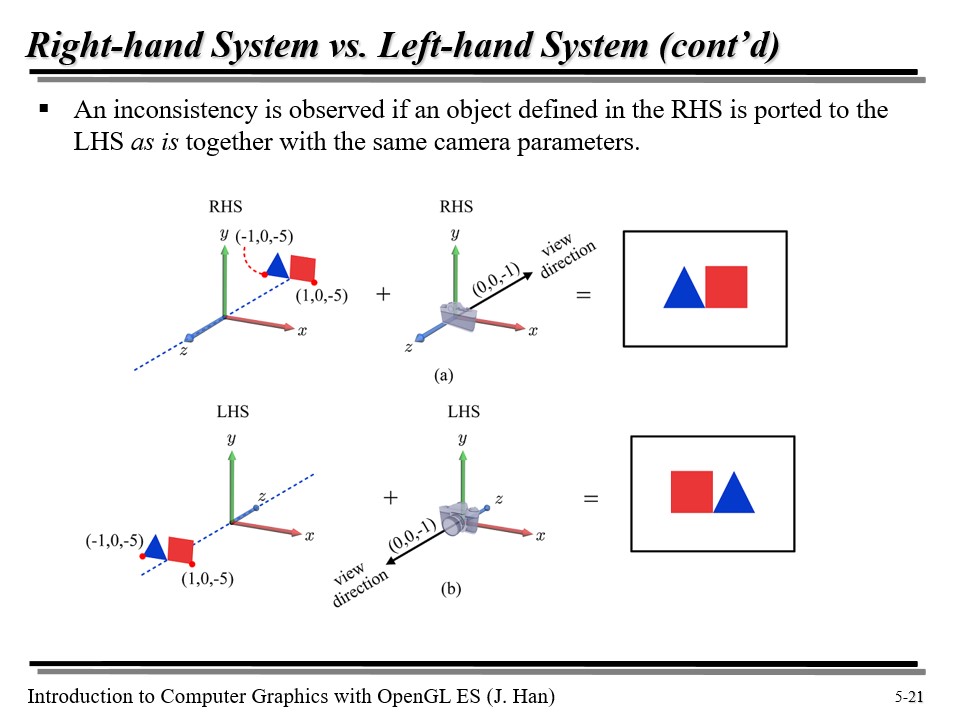
위 그림을 보자. 오른손 좌표계를 사용할 때, 카메라가 첫번째 그림처럼 있으면, 삼각형이 왼쪽에 그려진다.
그런데 아래처럼 왼손 좌표계를 사용할 경우, 사각형이 왼쪽에 그려지게 된다. 물체의 배치는 방향만 바뀌었음에도 불구하고 말이다!
 

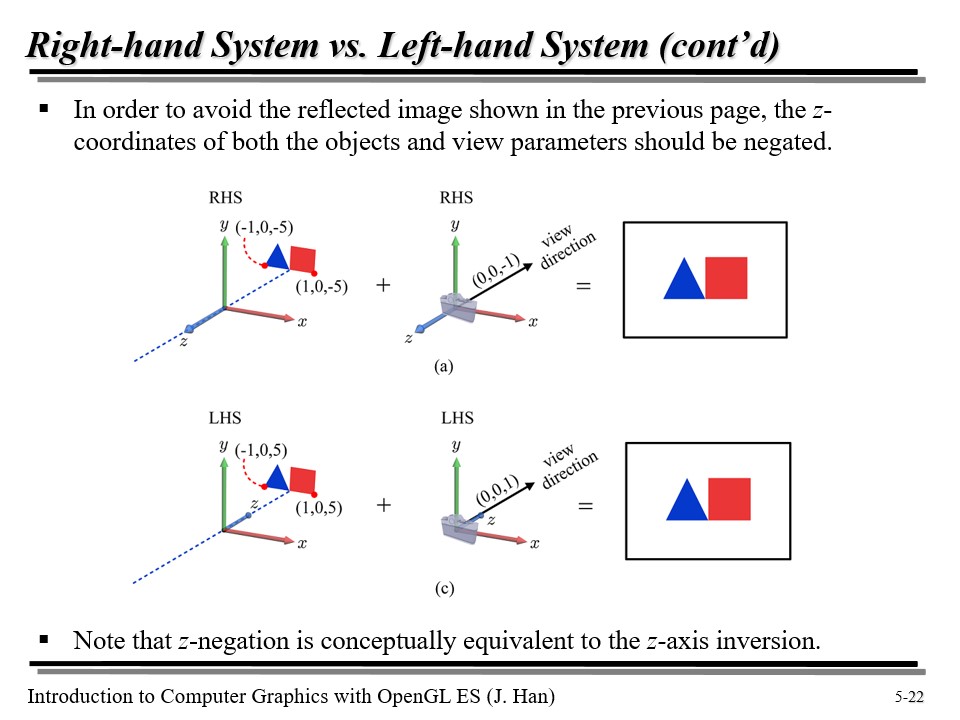
위 문제의 해결책은 사실 매우 간단하다. 그냥 물체의 z 좌표에 '-1' 을 곱해주면 된다!
 
 

절두체 (View Frustum)

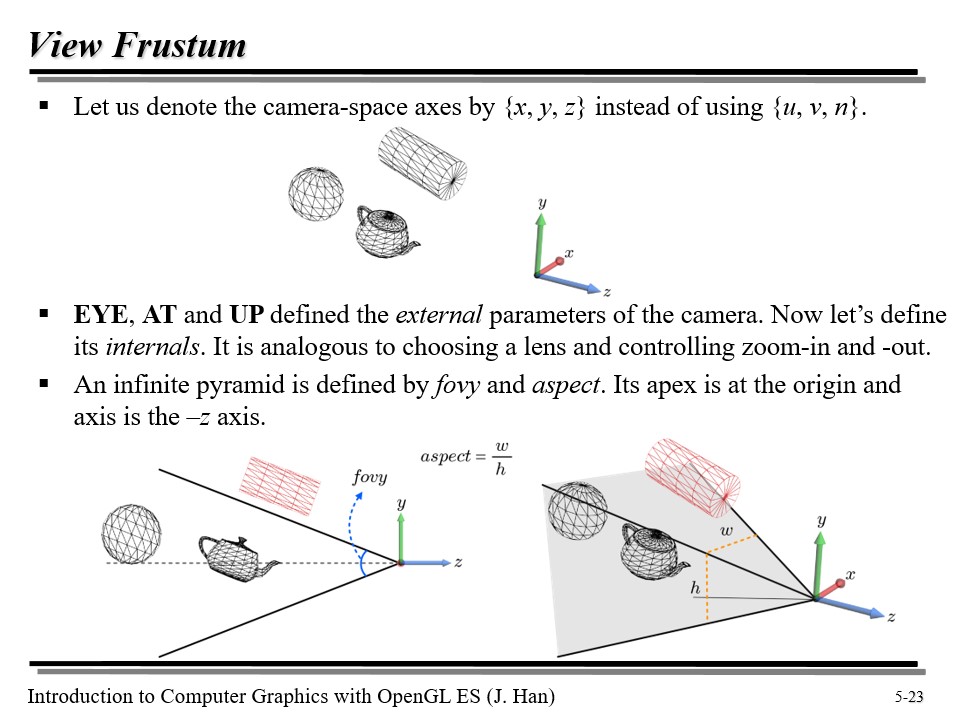
자, 지금껏 Vertex Shader 는 월드 변환과 뷰 변환을 수행해서, 우리는 현재 카메라 공간에 와 있다고 하자.
카메라 공간에서의 축을 친숙한 x, y, z 라고 다시 네이밍하자.
우리는 카메라를 찍을 때 일반적으로 줌인/줌아웃을 한다. 이것을 internal 이라고 부르기도 하는데, 이때 카메라에 담길 녀석들을 정하는 '피라미드형 공간'은 fovy 와 aspect 로 정의된다.
fovy 는 Field of View Y-axis 이다. 즉, y 축으로 얼마만큼의 시야각을 가질 것인지를 결정한다. aspect 는 종횡비로, y 축에 비해 x 축을 얼마나 볼 것인지를 결정짓는다.
위를 계산해서 나온 w(좌우) 와 h(높이) 를 이용해 피라미드를 정의할 수 있다!
 

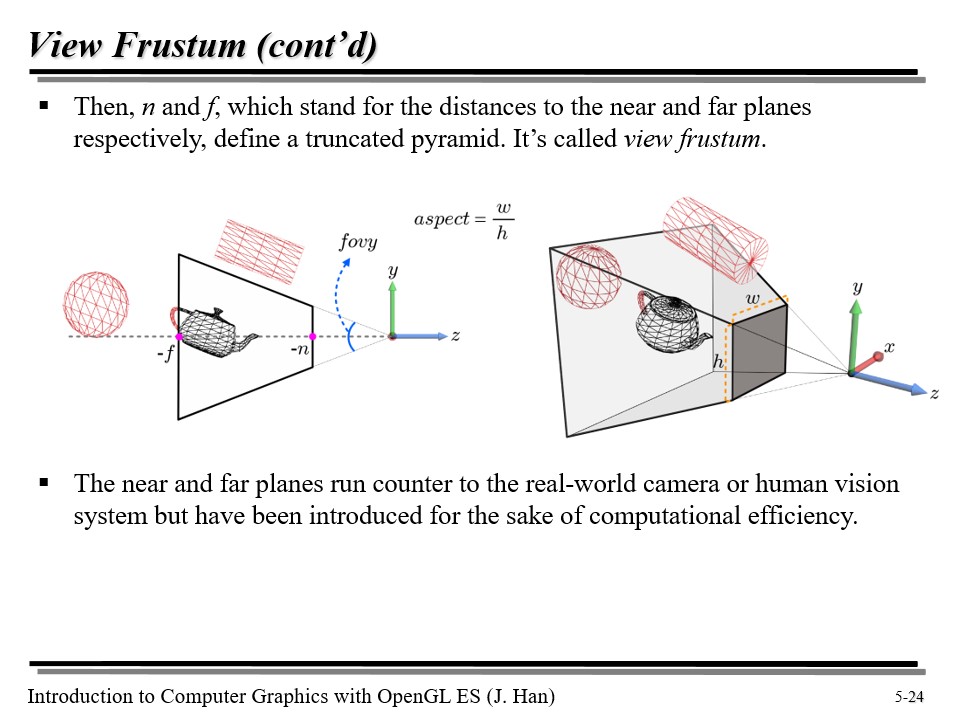
월드 공간에서 아무리 많은 오브젝트가 있던 간에 관계 없이, 카메라가 담아내는 영역은 한정되어 있다. 따라서, 해당 영역에 담기지 않는 오브젝트는 컬링된다. 이 영역을 절두체(View Frustum) 이라고 부른다.
 

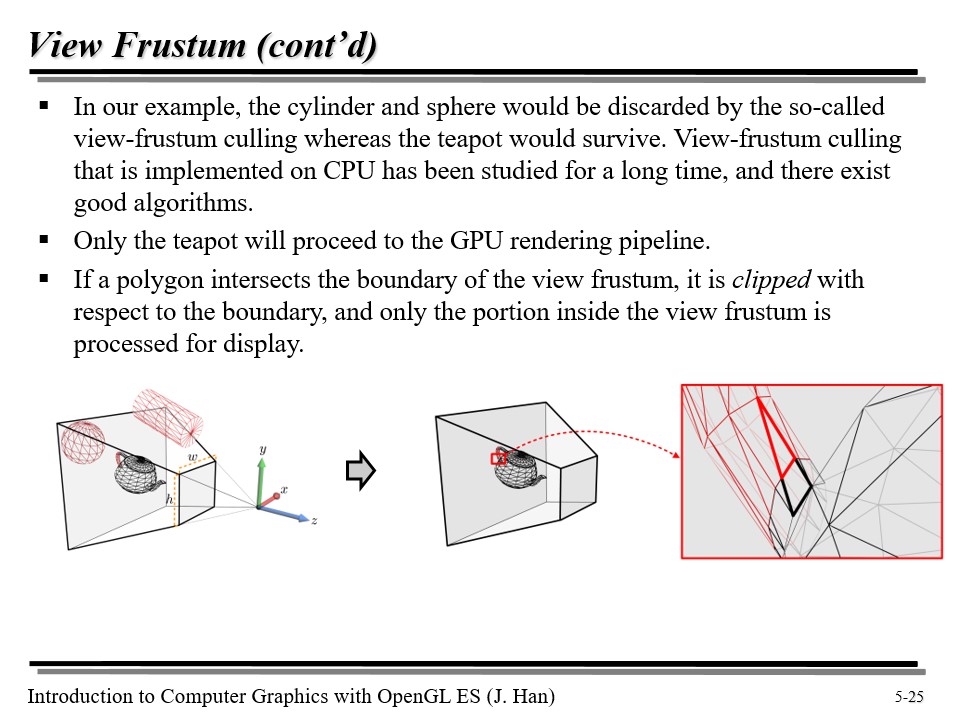
위 그림에서, 절두체 안에는 구와 원기둥이 들어오지 않으므로, 이 녀석들은 컬링된다.
그런데 주전자는 애매하다. 왜냐하면 손잡이 부분의 일부가 절두체 밖으로 나가 있기 때문이다. 이 녀석은 잘라내어야 하는데, 이것을 clipping 이라고 한다. 그렇다면 이 녀석은 어떻게 자를 수 있을까?
 
 

투영 변환 (Projection Transform)

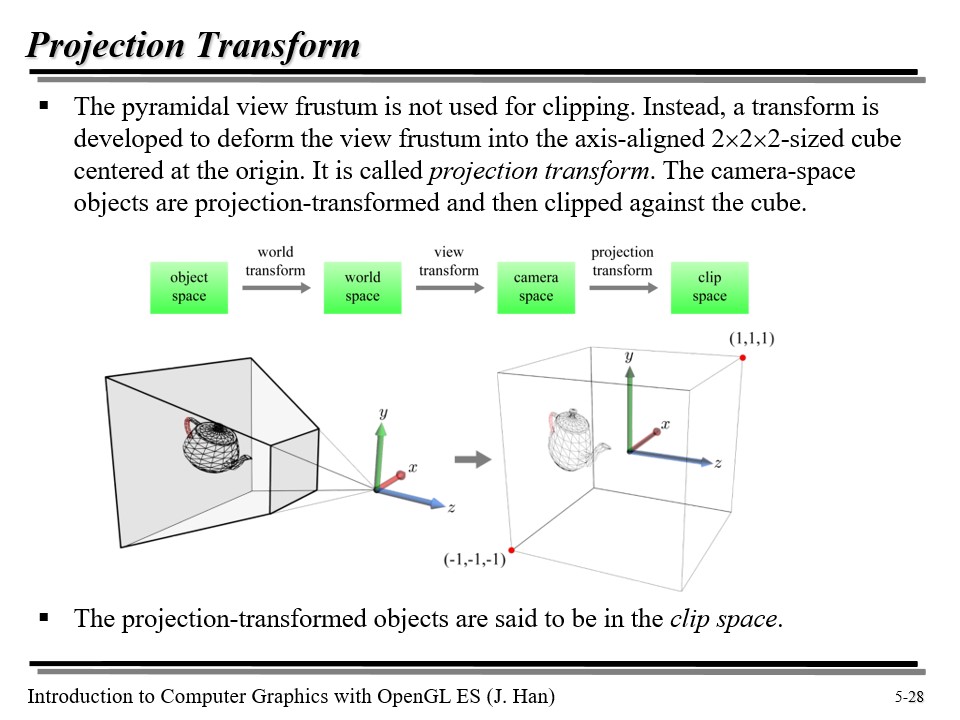
주전자의 손잡이 부분을 쉽게 자르기 위해, 우리는 절두체를 정육면체 공간으로 변환한다. 왜냐하면 단면이 축과 평행해 지기 때문이다! 위처럼 절두체를 정육면체로 바꾸는 변환을 projection transform 이라고 하며, 그 공간을 clip space 라고 부른다.
 

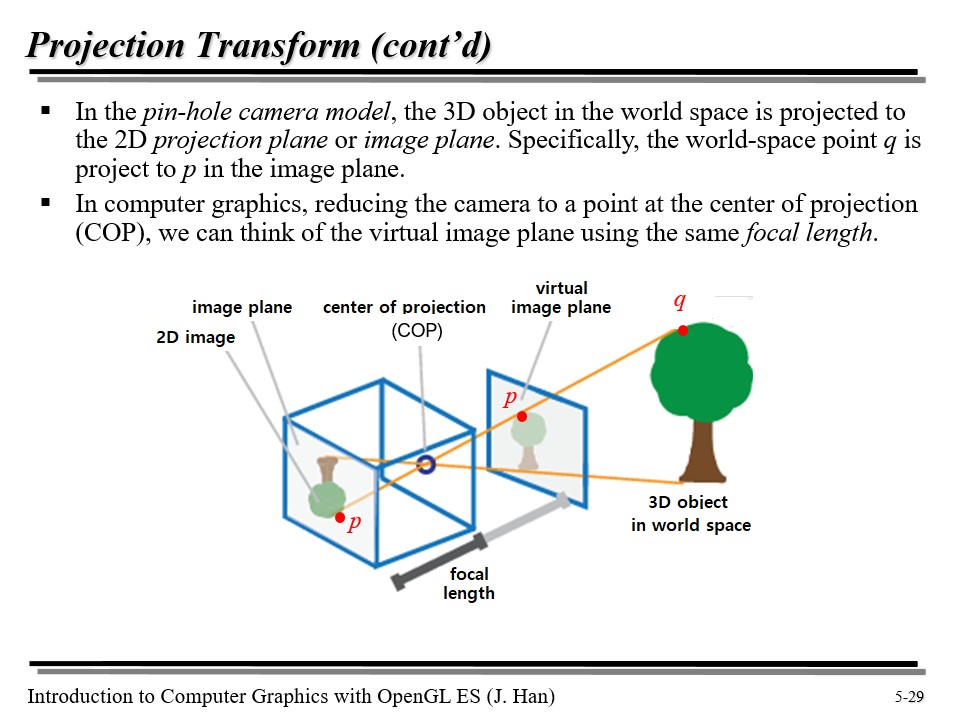
위에서 카메라가 마치 COP(Center of Projection)에 있는 것처럼 만들면, virtual image plane 을 같은 focal length 를 이용해 표현할 수 있다.
 

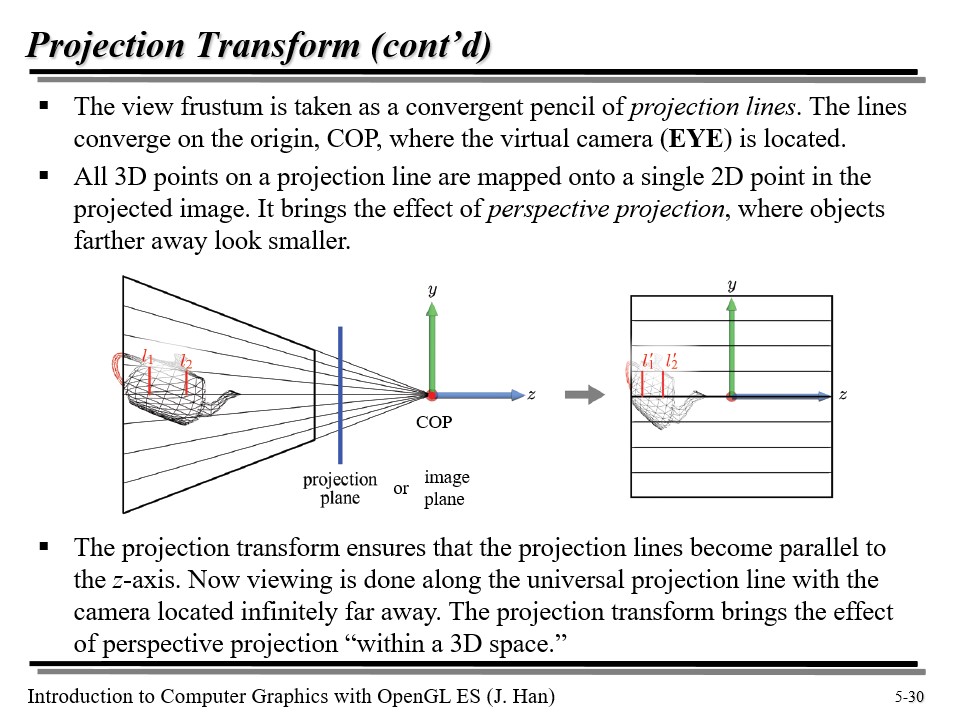
실제 카메라라고 하면, COP 에 상이 맺힌다. 이 때, projection plane 을 만들면, 해당 단면에 투영되는 주전자는 위의 오른쪽 그림처럼 나올 것이다.
이때, l1 과 l2 는 길이가 달랐지만, projection plane 으로 오면서 길이가 l1', l2' 로 같아지게 된다!
물론 그래픽스에서는 위처럼 2D 로 변환하지는 않고, 3D 로 변환하면서 원근을 보존한다 😁. 위의 설명은 기본적인 개념만 설명한 것이다.
 

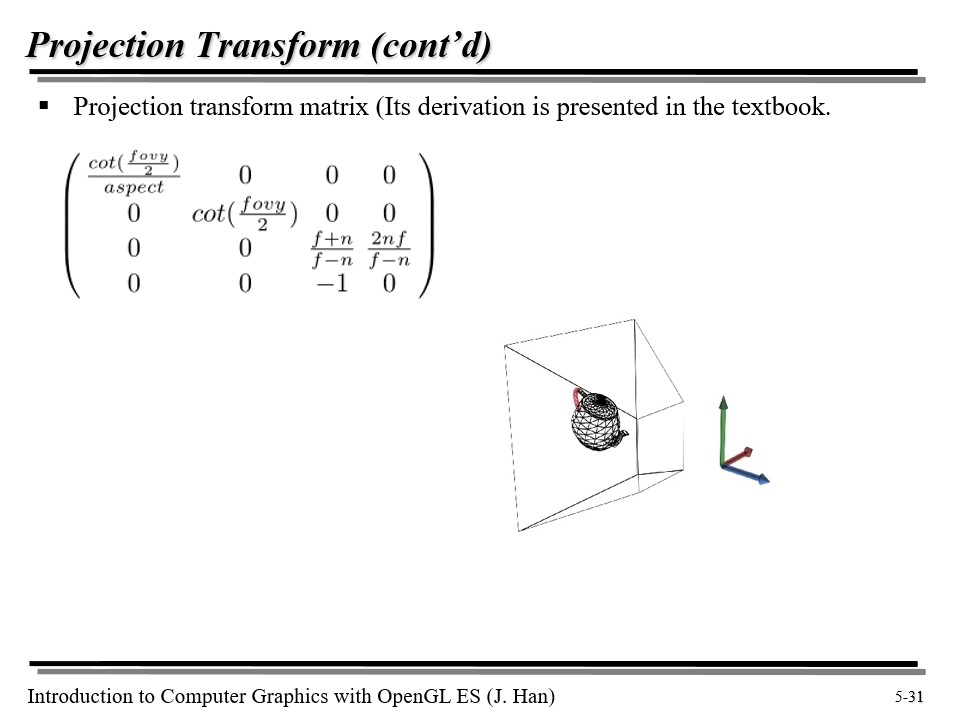
투영 행렬은 위와 같은데, 따로 증명을 하지는 않겠다. 궁금하면 찾아보도록 하자 😅
 

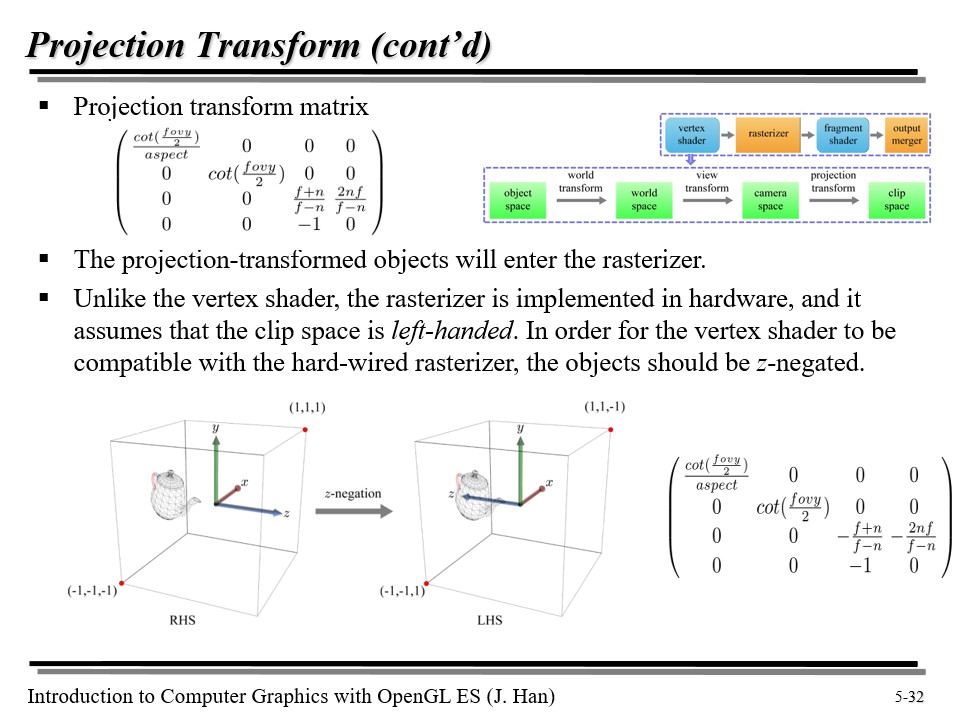
이제 우리는 vertex shader 의 동작을 모두 알아봤다.
공간 변환에서 월드 공간으로, 다시 카메라 공간으로, 마지막으로 클립 공간으로 물체를 변환시켰다.
vertex shader 는 오른손 좌표계를 사용했다. 그런데 다음 단계인 rasterizer 는 왼손 좌표계를 사용한다. 따라서 vertex shader 가 전달한 행렬에서 z 축 값의 부호를 바꿔 주어야 한다!
그런데 결과값을 바꾸기 보다, 그냥 projection transform 에 필요한 행렬을 곱해줄 때, z 축에 부호가 바뀐 상태를 곱해주는게 더 편하다. 따라서 아래와 같이 projection transform matrix 의 z 축 쪽 부호를 바꿔서 곱해준다 😉

 

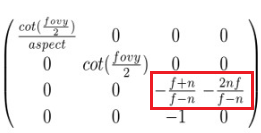
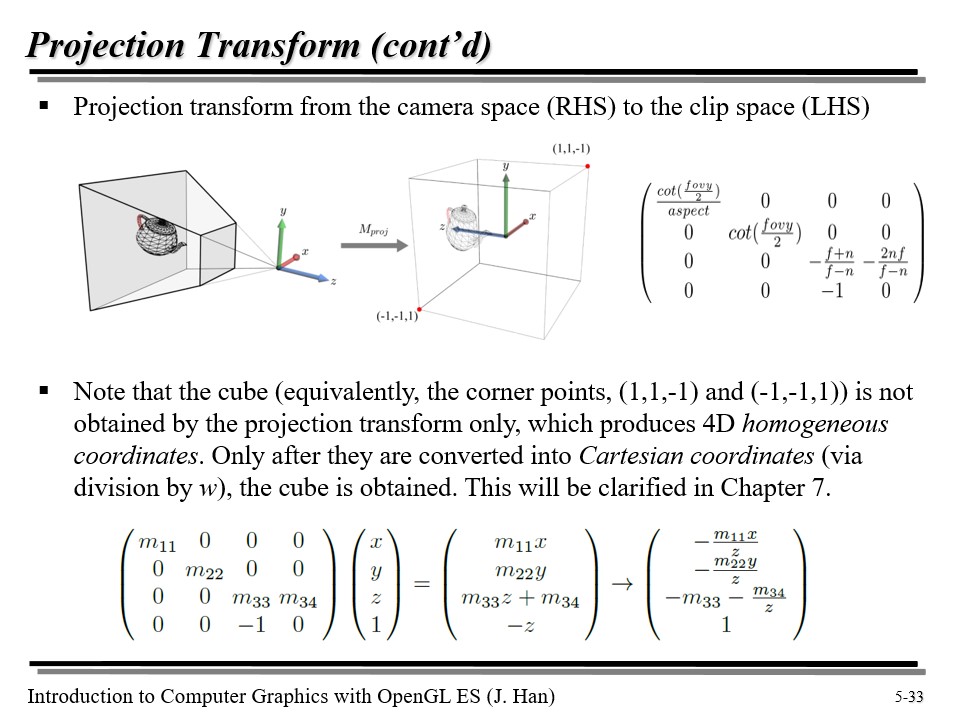
위의 슬라이드에 대한 설명은 7강에서 자세히 다룰 것이다 😇