[OpenGL ES] 12강 : Object Picking, Ray Intersection, Bounding Volume, Arcball

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

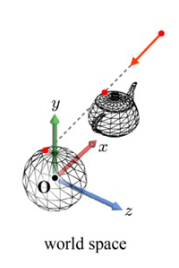
1. 오브젝트 피킹(Object Picking)을 하면, 스크린 스페이스에서 Ray 를 z 축 방향 안쪽으로 쏜 다음, 처음으로 부딪히는 오브젝트를 선택되었다고 인식한다. 이 Ray 를 Object Space 로 바꾸기 위해 3번의 변환(Screen -> Camera -> World -> Object)을 진행해야 한다(각 Ray 에 대해 Object 별로 Ray 가 생성)

2. 오브젝트 피킹에는 Ray Intersection(폴리곤 메시에서 Ray 가 삼각형 안에 있는지 체크) 과 Bounding Volume 방식이 있다. Bounding Volume 방식은 간단하면서 효율적이므로 전처리 과정에서 적용하고, 상세 체크를 위해 Ray Intersection 을 사용하면 된다.

3. 물체를 회전시키기 위해서 아크볼(Arcball) 의 개념을 사용한다. 이는 물체를 감싸고 있는 구가 있다고 가정하고, 해당 구를 돌리는 것과 물체를 돌리는 것이 연동되어 있다고 가정하는 방식이다.

오브젝트 피킹(Object Picking)

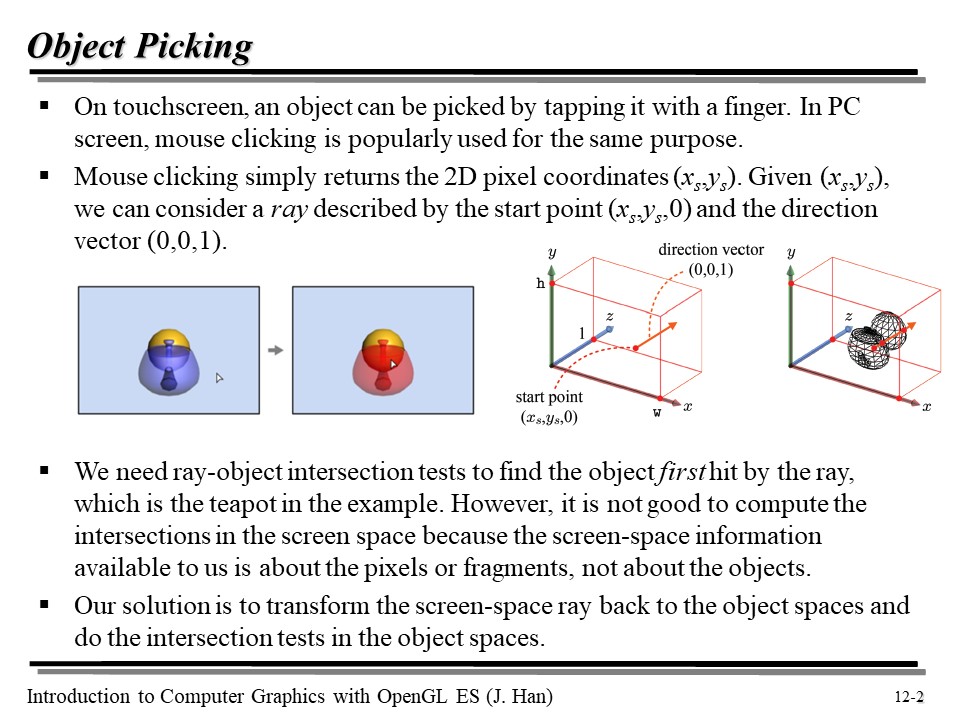
게임을 하다 보면, 화면에 있는 물체를 클릭할 때가 있다. 그런데 잘 생각해보면, 사실 우리는 물체를 직접 선택했다기 보다는 스크린 공간의 한 픽셀을 누른 것인데, 이게 어떻게 가능한 것일까?
스크린 위의 한 점을 선택한다고 해 보자. 이때, 해당 점에서 z 축 안쪽 방향으로 Ray 를 쏜다고 해 보자. 그럼 해당 Ray 와 '처음으로' 마주치는 물체가 있을 것이다. 바로 그 녀석이 위에서 선택된 주전자 같은 오브젝트라고 생각하면 된다.
그런데 사실 레이와 오브젝트가 교차하는지를 체크하는 것은 쉽지 않다. 왜냐면 pixel 과 fragment 에 대한 정보는 오브젝트별로 클러스터링되어 있는 것이 아니라, 그냥 각각의 픽셀과 fragment 정보값으로 분해되어 스크린 스페이스에 흩뿌려져있는 것이기 때문이다.
따라서 우리는 스크린 공간에서의 ray 를 다시 object space 로 변환한 후, 해당 ray 가 오브젝트와 교차하는지를 체크해야 한다.
 

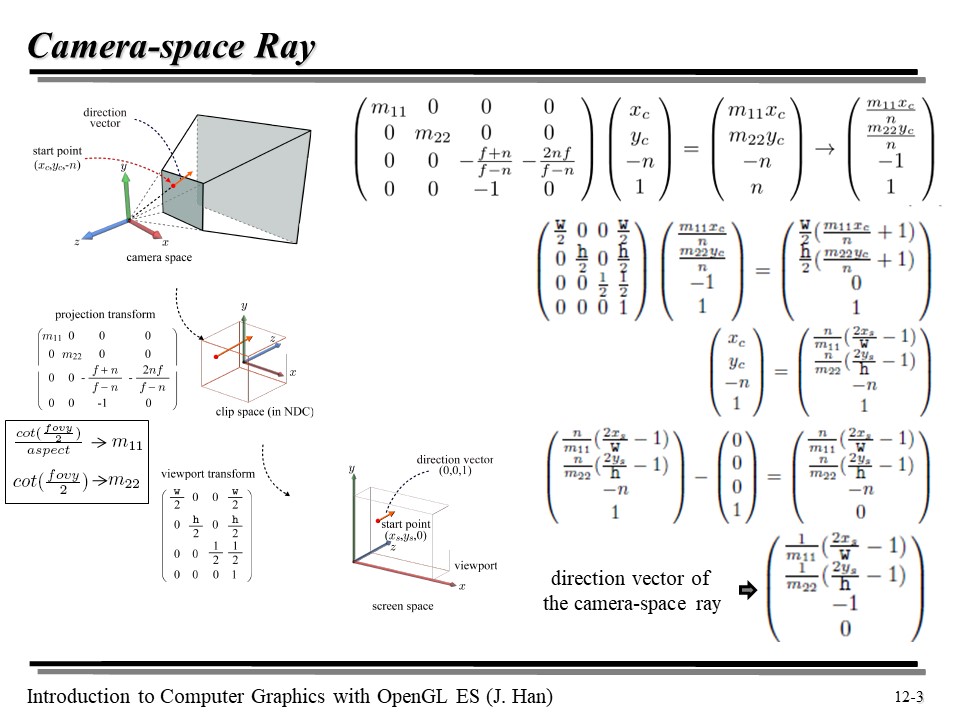
위의 그림에서는 Camera Space -> Clip Space -> Screen Space 로의 변환을 시각적으로 보여주고 있다. 그런데 Screen Space 에서의 Ray 를 Camera Space 로 어떻게 변환할까? 😅
일단 시작점부터 보자. Ray 의 start point 는 (xs, ys, 0) 으로 정의해 놓았는데... 이 녀석을 Camera Space 로 바꾸어야 한다.
위의 첫 줄은, Camera Space 를 Clip Space 로 옮기는 변환을 의미한다.

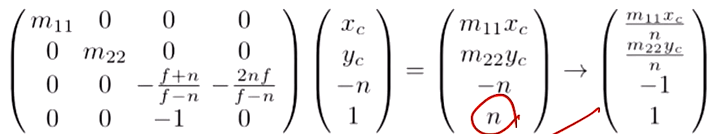
왼쪽의 행렬이 Projection Matrix 이다.

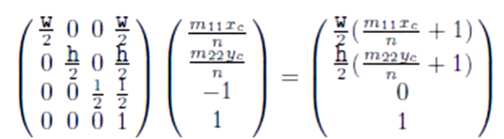
두 번째 줄은 NDC 공간으로 옮기기 위한 변환을 의미한다(폭이 2인 정육각형의 공간으로... 그리고 원점을 옮기는 변환).

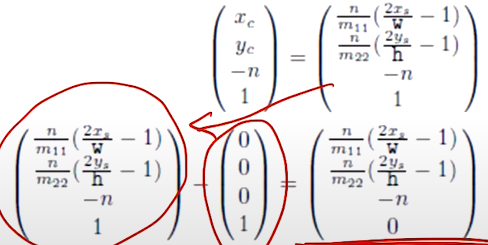
카메라 스페이스에서의 출발점은 (xc, yc, -n, 1) 로 표현되는데... 여기서 (0, 0, 0, 1) 을 빼면, 즉, 원점을 빼면, 우리는 벡터를 구할 수 있다. 어떤 벡터? 바로 원점에서 출발점으로 가는 벡터를! (a - b 는 a <- b 벡터로 생각하라고 누누이 얘기했었다 😉)
따라서, 우리는 Camera space 에서의 ray 를 구할 수 있게 되었다! 

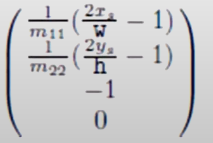
제일 마지막 값에서 각 항을 n 으로 나눈 결과가 바로 위의 항이다.
 

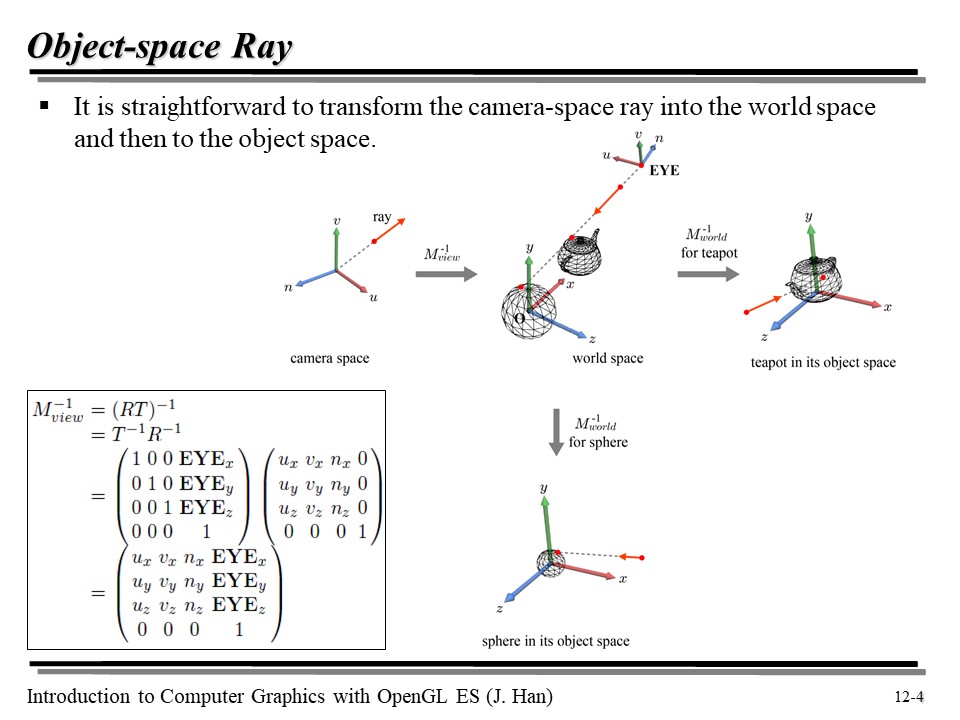
자, 이제 카메라 공간까지 왔으니 월드 공간으로 가보자. 이전에 World Space 에서 Camera Space 로 갈 때는 View Transform 을 취했었다. 즉, 기존의 RT 에 inverse 만 취해주면 Camera Space 가 World Space 로 바뀌게 된다.

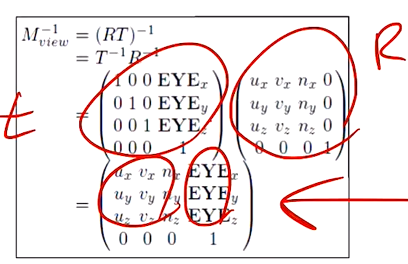
R 과 t 로 나뉘었는데... 우리는 이미 R 을 먼저 계산하고, t 는 나중에 계산하면 된다는 것을 알고 있다 😄
자 그럼 이제 Ray 를 World Space 로 옮겼다. 이제 이 Ray 를 어떻게 하면 Object Space 로 바꾸어야 할까? 사실 너무나 간단하게도, 월드 공간으로의 변환 행렬의 역행렬을 곱해주면 된다!

다만 하나 기억해 둘 것은... 물체 각각이 World Transform 을 갖고 있으므로, 하나의 world-space ray 마다, 각각의 오브젝트의 ray 가 각각 다르게 정의된다는 것이다! 😮
 
 

Ray Intersection

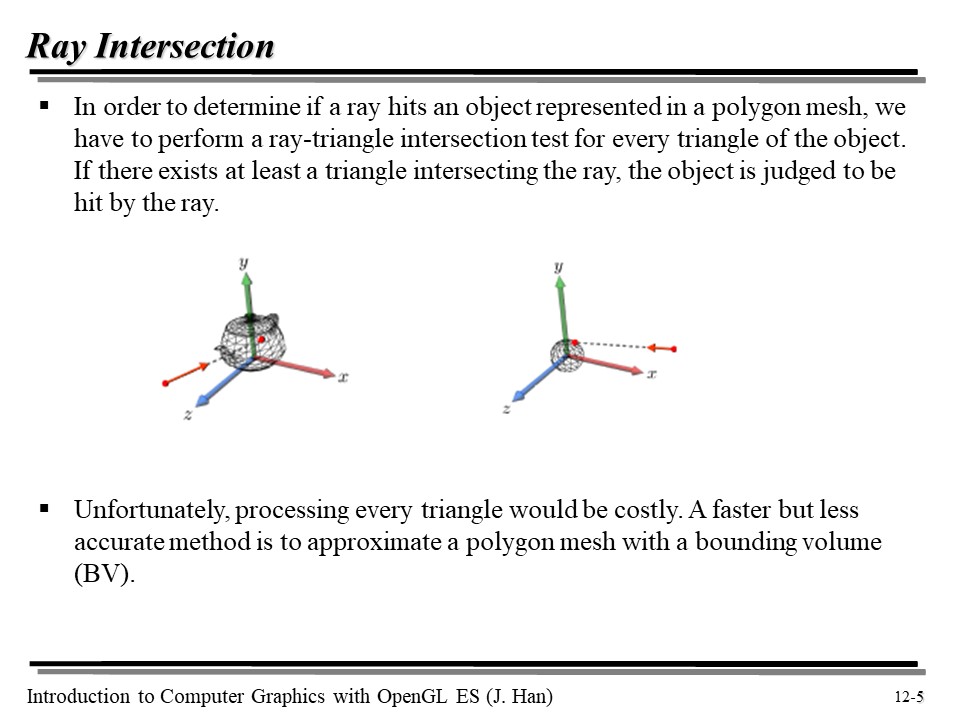
우리는 이전에 Ray 가 Polygon mesh 와 부딪히는지 검사했다. 이는 오브젝트의 모든 삼각형에 대해 ray-triangle intersection test 를 해야 하므로, 비용이 매우 크다.
덜 정확하긴 하지만, 효율적인 방법으로 Bounding Volume(BV) 가 있다!
 
 

Bounding Volume

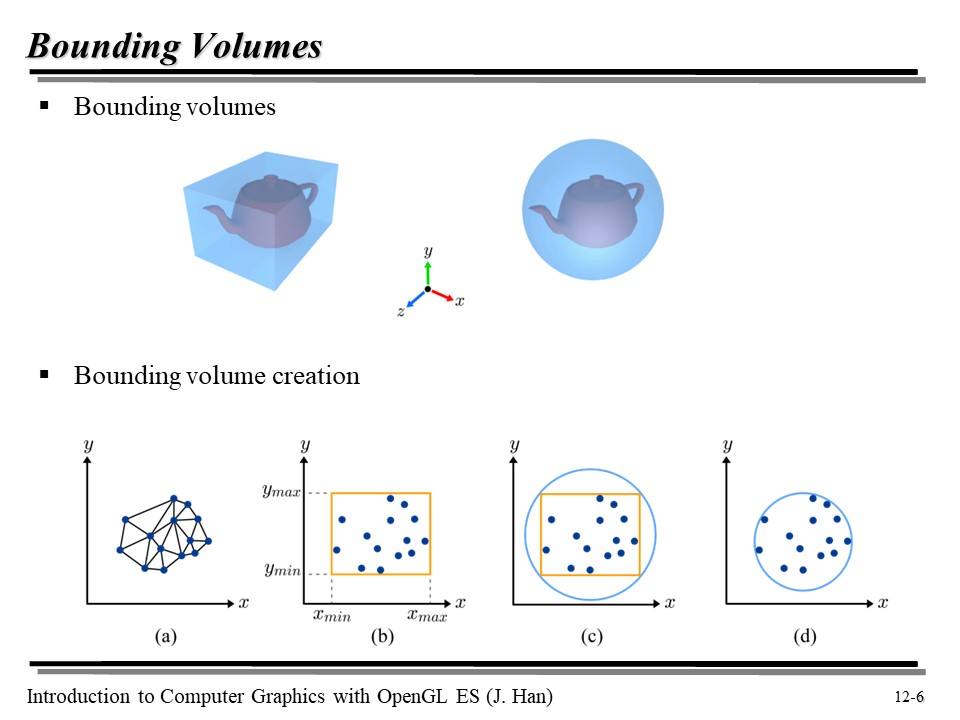
Bounding Volume 은...

라고 정의된다. 위에서 주전자를 각각 box 와 sphere 로 정의했다.
Bounding Volume 을 만드는 방식은 위의 사각형과 원 그림으로 잘 나타나있다. 물론 추상화가 많이 들어간 버전일 것이지만... 🤣
 

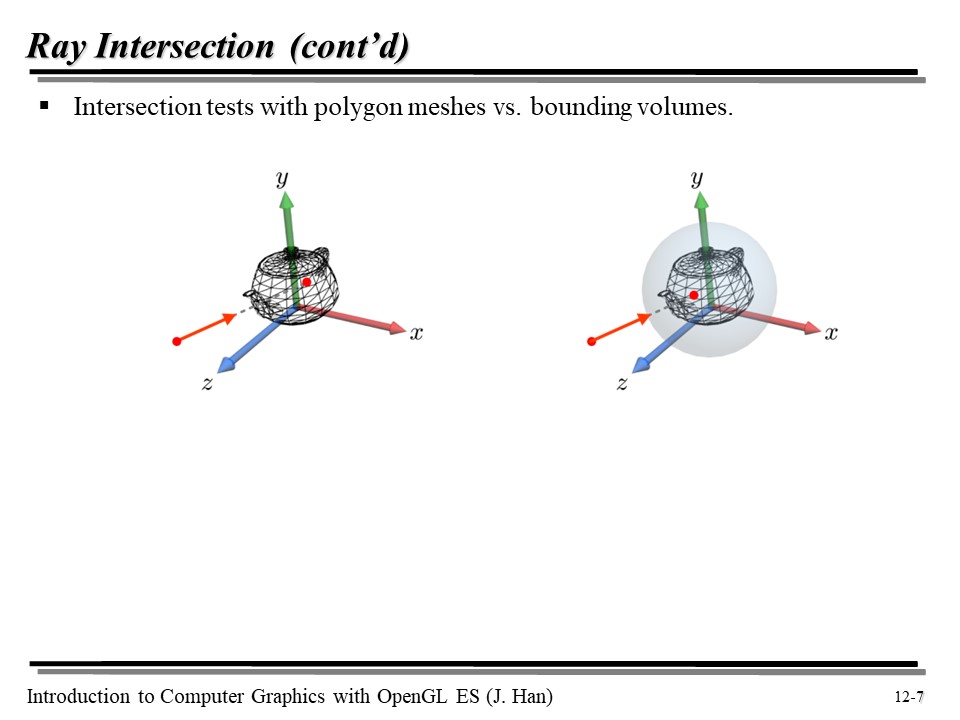
두 방식을 비교하면... polygon mesh 에 intersection test 를 하면 정확하지만 연산량이 많고, bounding volume 을 쓰면 간단하지만 부정확하다는 단점이 있다.
 

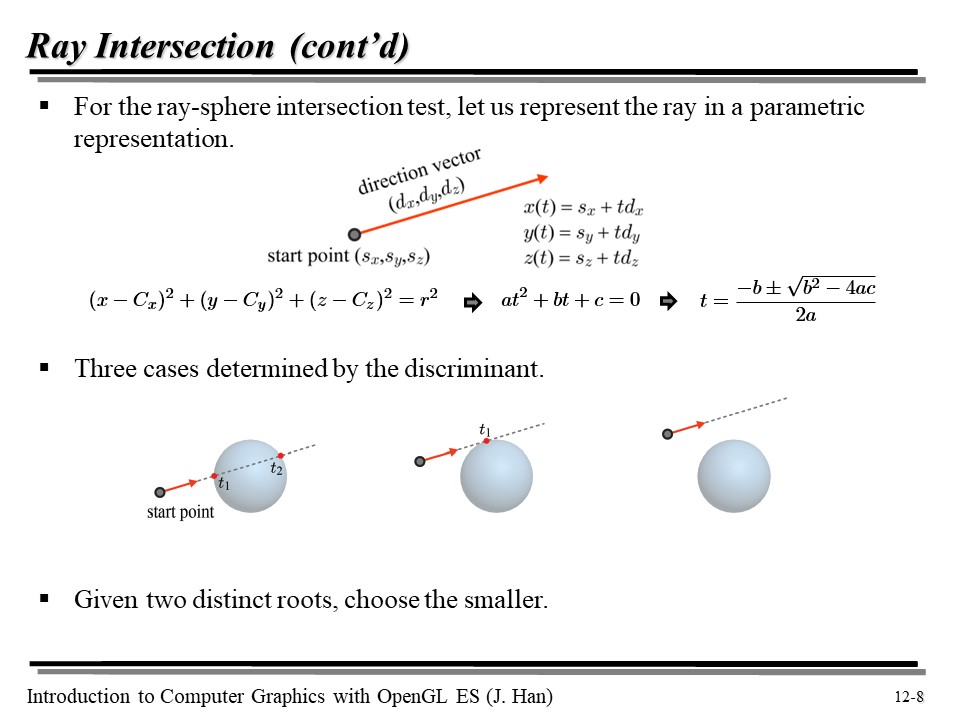
Ray 를 수학적으로 표현하면... 그냥 직선의 방정식으로 표현할 수 있다.

Bounding Volume 은 그냥 구의 방정식이다.

이 두 식을 그냥 연립하면 된다. 방정식은 t 에 대한 식이다.

이때, 근이 두 개면, 작은 값이 당연히 먼저 부딪힌 지점일 것이다.
 

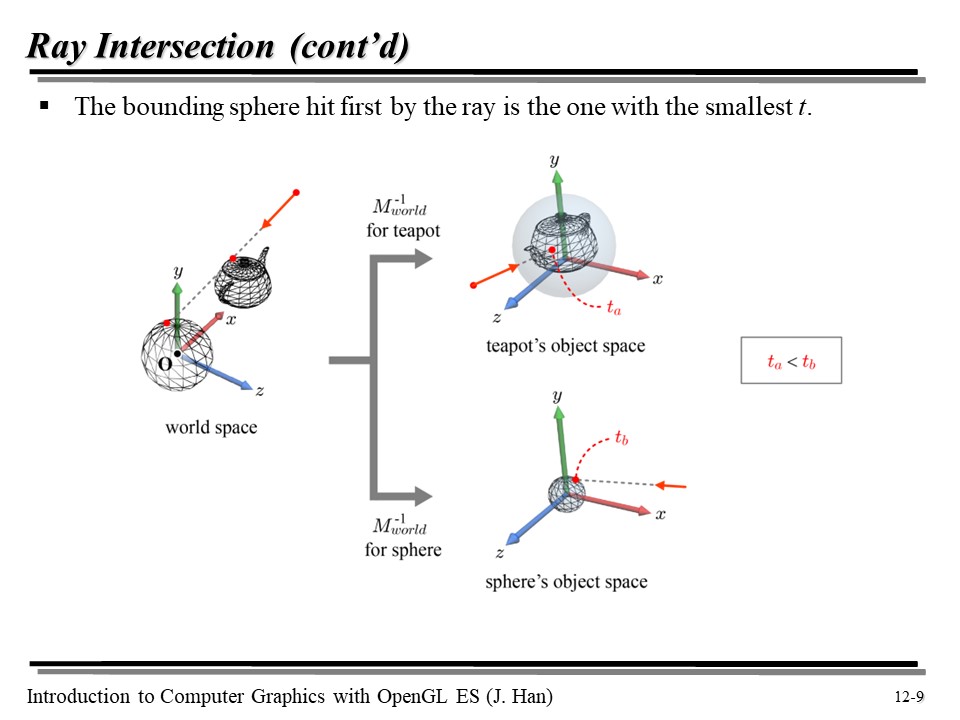
위에서, ta, tb 를 World Space 에서의 Ray 가 주전자와 원을 부딪혔을 때의 t 값이라고 하자.

바로 위의 주황색 Ray 이다. 이때, ta < tb 이면, 그냥 주전자가 먼저 부딪혔다고 이해하면 된다!
 

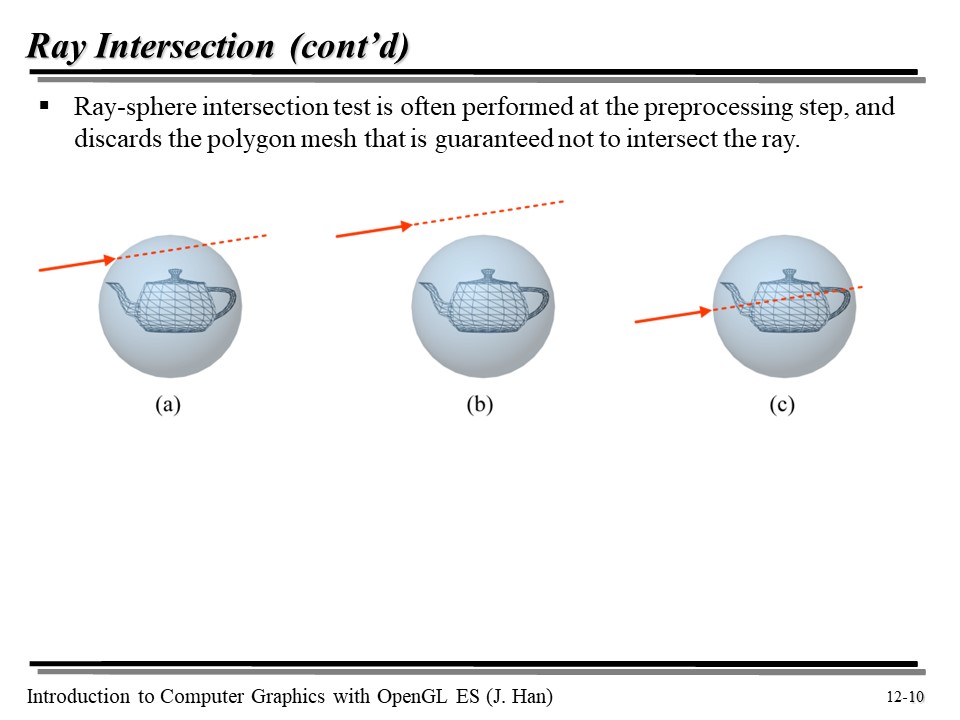
근데 BV 를 이용한 테스트는 부정확하다. 하지만 BV 를 전처리 단계에서 먼저 사용하면, 절대 충돌하지 않을 오브젝트에 대해 불필요한 intersection test 를 하지 않아도 된다는 것을 잘 알 수 있다! 따라서 BV 를 같이 사용하면 좋다! 🤗
 

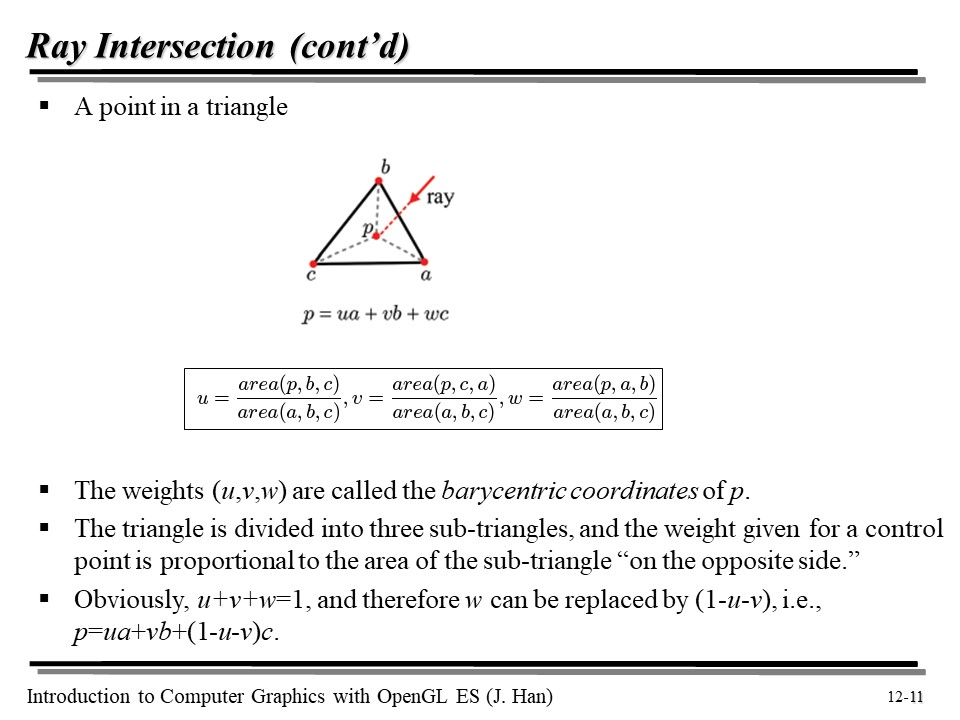
Ray 가 삼각형 한 점 p 와 부딪혔을 때, 점 p 가 각 꼭짓점 a, b, c 와 얼마나 가까운지를 넓이의 비를 이용해 표현할 수 있다. 이를 각 u, v, w 라고 하고, weight 라고 하자.

이 (u, v, w) 를 p 의 barycentric coordinates 라고 한다. u + v + w = 1 일 것이며, u, v, w 각각은 다른 두 변수로 표현이 가능할 것이다... w = 1 - u - v 처럼!
 

s + td 로 정의된 ray 와 삼각형의 intersection 은 다음 두 식의 연립해서 풀 수 있다 :

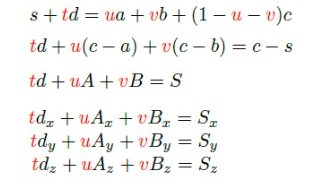
식을 잘 따라가면, w 를 u, v 를 이용해 치환하여 t, u, v 에 대한 식으로 표현했다.
어라... c - s 가 갑자기 왜 S 가 되고 S 가 왜 Sx, Sy, Sz 로 쪼개지지.. 라고 생각할 수 있는데, 생각해보면 간단하다.
a, b, c, 는 3차원 좌표이고, d 는 3차원 공간에서의 벡터이다. (s 는 시작점이니까, 3차원 좌표).
그래서, 각 좌표의 x, y, z 값을 따로 계산한다는 의미로 식 3개로 쪼갠 것이다 😉

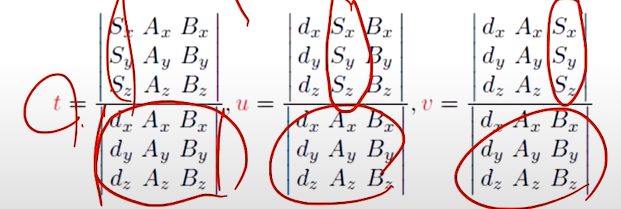
이제 Cramer's Rule 을 사용하면 적절한 t, u, v 를 구할 수 있다(크레이머 룰은 검색하자 😂).
그런데 사실 우리는 정확한 p 를 구하는게 목적이 아니라, 교차 했는지 여부가 중요하다. 그럼 p 가 삼각형 안에 있는지... 어떻게 알 수 있는걸까?

 

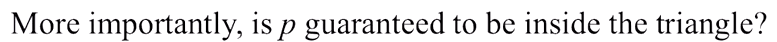
교차점 p 가 삼각형 안에 있으려면, u >= 0, v >= 0, u + v <= 1 의 조건을 만족해야 한다. 그래야만 상대적 무게값을 고려해 봤을때 p 가 안에 존재할 것이다.

 

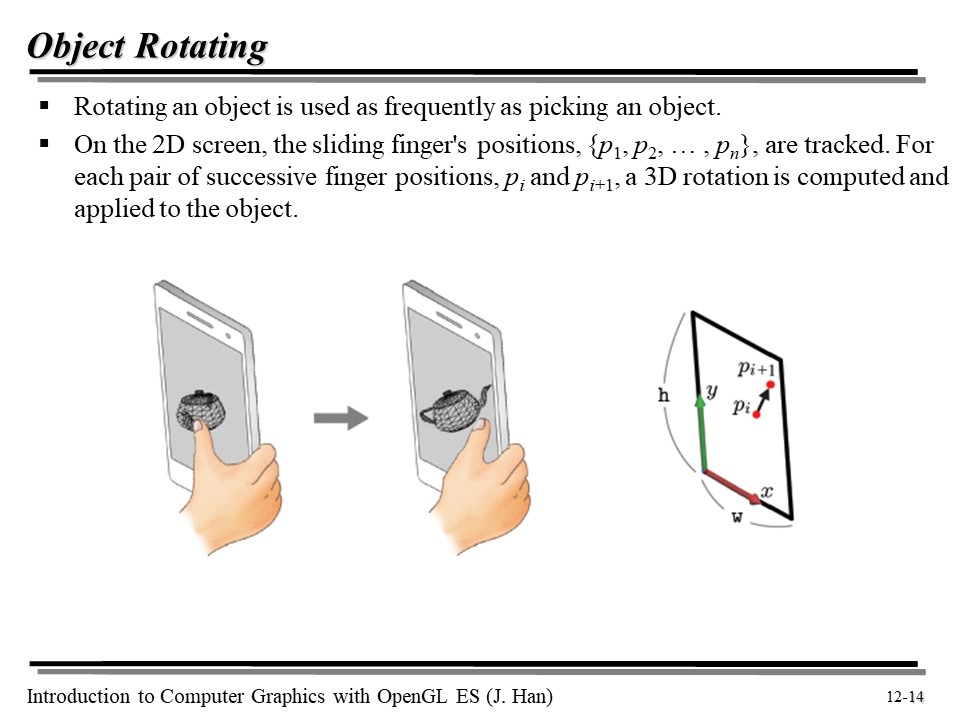
그럼 스크린 공간에서, 오브젝트의 회전은 어떻게 가능한 것일까?
 
 

아크볼 (Arcball)

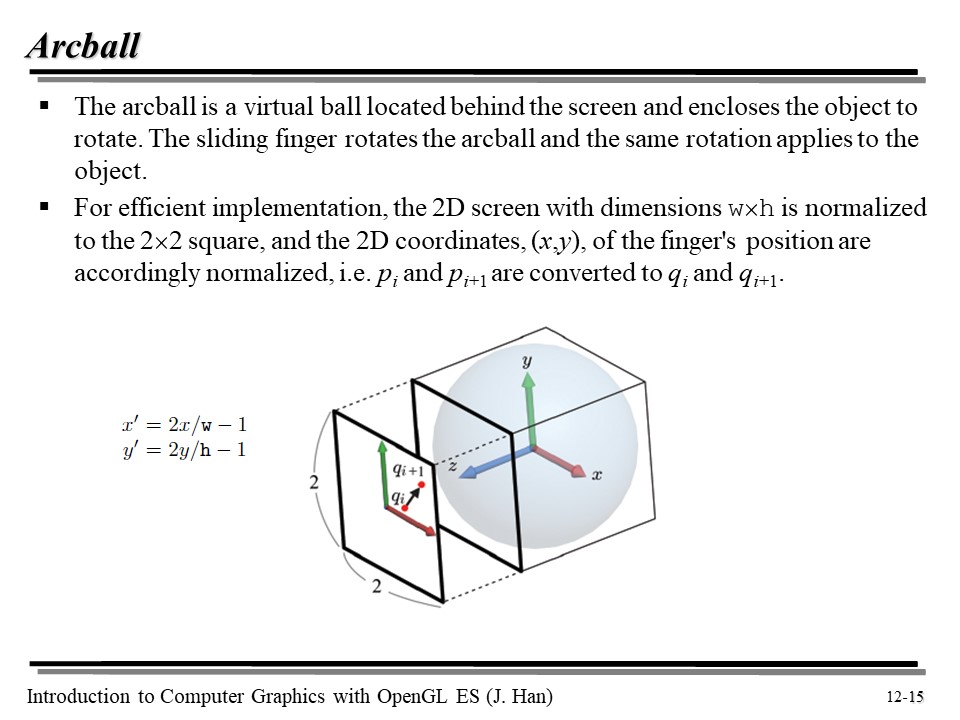
간단하게 생각해서, Arcball 이라는 개념을 적용할 수 있다. 오브젝트와 연동되어 돌아가는 원을 정의하고, 해당 원이 오브젝트가 감싸고 있다고 하자. 이제 오브젝트를 회전하는 것과 Arcball 을 회전하는 것은 같은 동작이 된다.
효율적인 구현을 위해, 일단 공간을 normalize 시키자 : (x -> x', y -> y' 로)

 

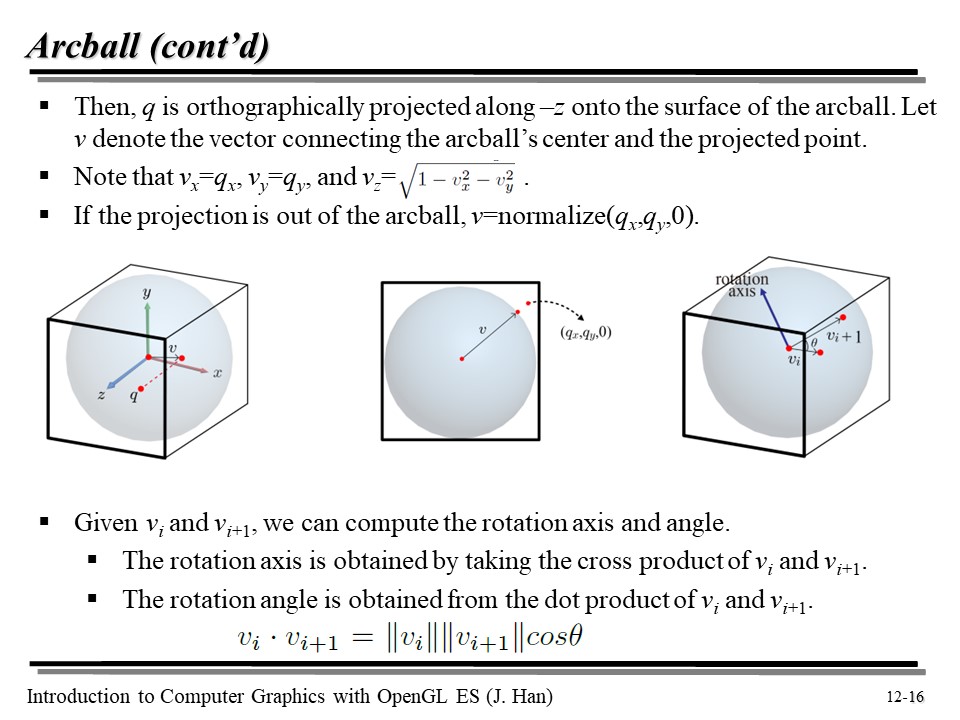
자, 위에서, 스크린 위의 점 q 를 원에 projection 시키고, 원점으로부터 해당 점까지의 벡터를 v 라고 하자.

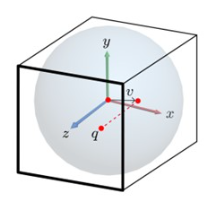
vx, vy 를 각각 qx, qy 라고 놓고, 다음과 같은 식을 만들자 :

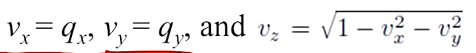
이제 다음과 같이 회전을 했다고 치자 : (vi 에서 vi+1 점으로)

 회전각 𝛉 는 내적을 취한 후, arccos 을 적용하면 쉽게 구할 수 있다. 그리고 rotation axis 는 외적을 통해 만들 수 있다.
 

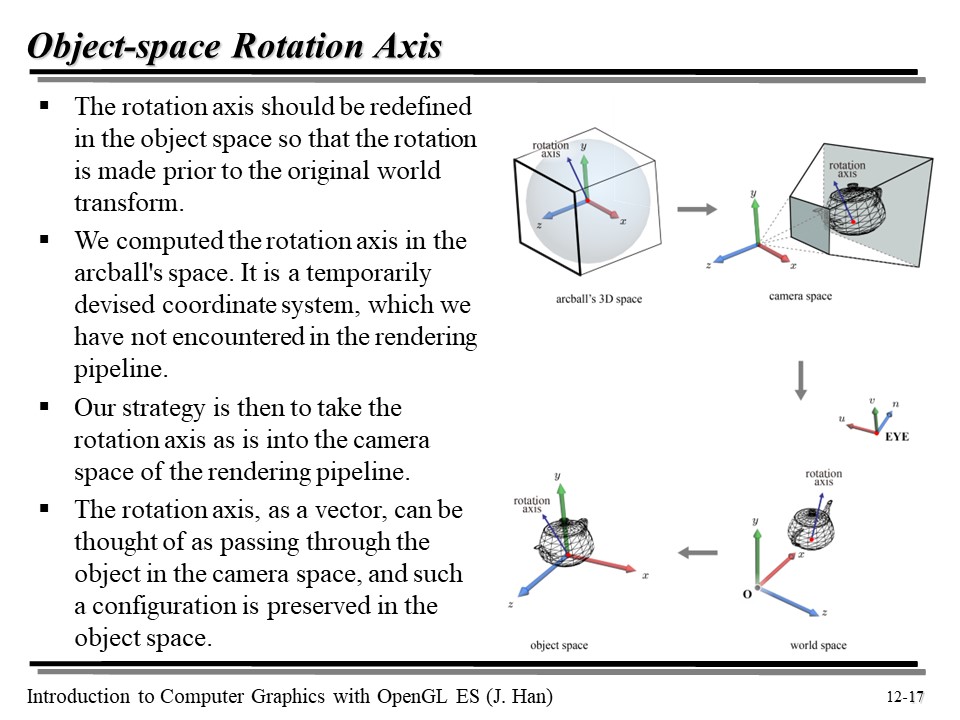
그런데 Arcball 의 공간은... 무슨 공간일까? 렌더링 파이프라인과 결합해야 하는데...

트릭으로는... 아크볼 공간에서 정의된 회전 축을 그대로 카메라 공간으로 옮기는 것이다. 이게 말이 되는 게... 우리가 물체를 보면서 회전을 했던 것 처럼, 카메라 공간에서도 카메라가 아크볼을 관찰하고 있다. 즉, 눈을 카메라라고 생각하면... 벡터니까 또이또이 하다.
그럼 Rotation Axis 에 World Space 로 역변환 하고, 다시 Object Space 로 역변환하면 회전을 제대로 적용할 수 있을 것이다! Rotation Axis 있고, 각도가 있으면... Quaternion 을 이용해 회전을 적용할 수 있다! 😊

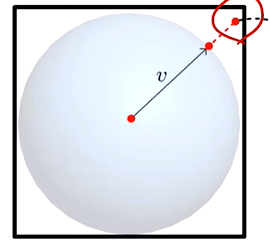
그런데 손가락이 아크볼 밖으로 나가면... 어떻게 될까? 이때는 그냥 Normalize 를 시켜서, 아크볼 위의 공간에 투영시키면 된다! 물론 그렇게 하다보면 회전이 안되는 경우도 있다 😅
 

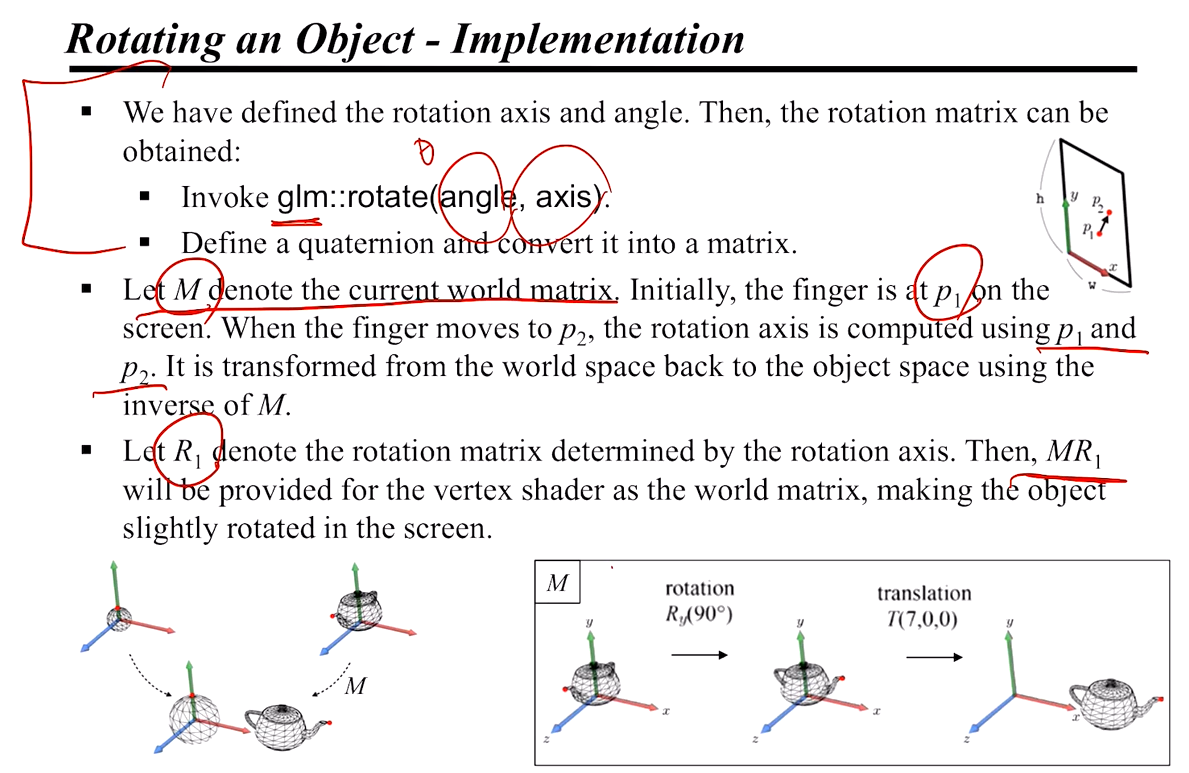
구현은 위와 같다. 이때, M 은 월드 공간으로 오브젝트를 변환한 행렬일 것이다. 그 후에 회전 행렬 R1 이 곱해져 실제 회전이 일어난다!
 

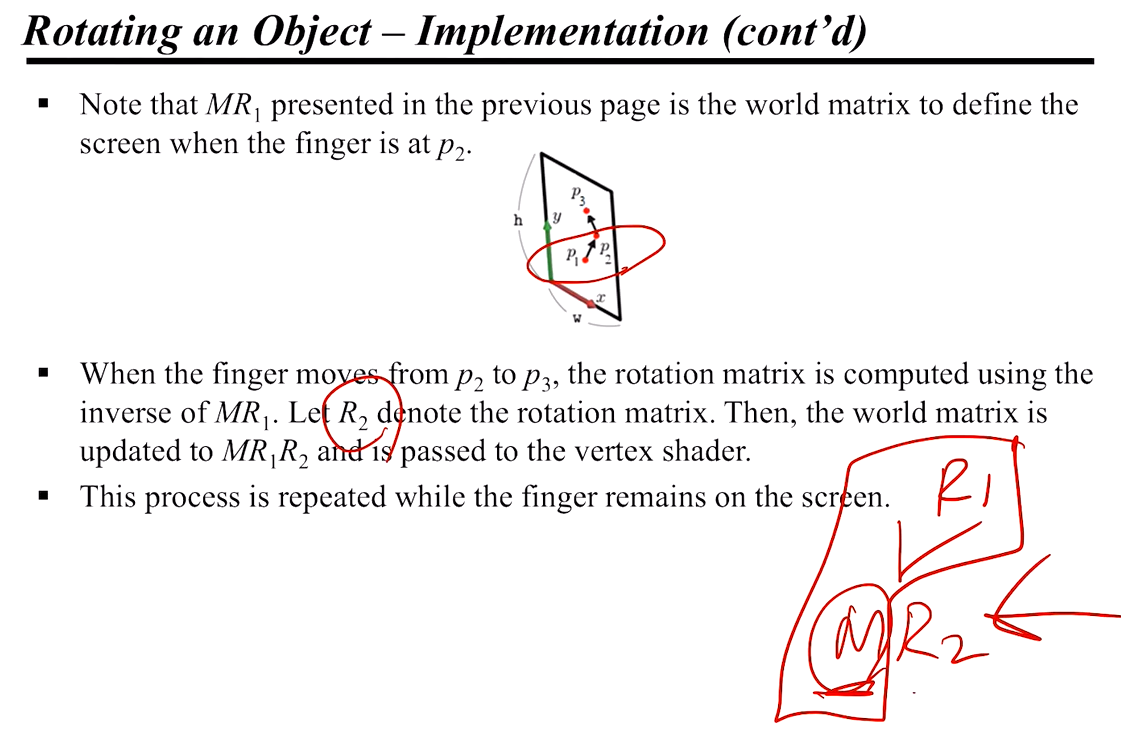
위처럼, p1 -> p2 -> p3 까지 회전이 적용되면... p2 시점에서는 위에서 설명한 World Matrix 인 M 이 MR1 인 것으로 생각해서 렌더링이 진행될 것이다 🙃